矩阵范数与人脸识别：张逸凯的计算机科学笔记

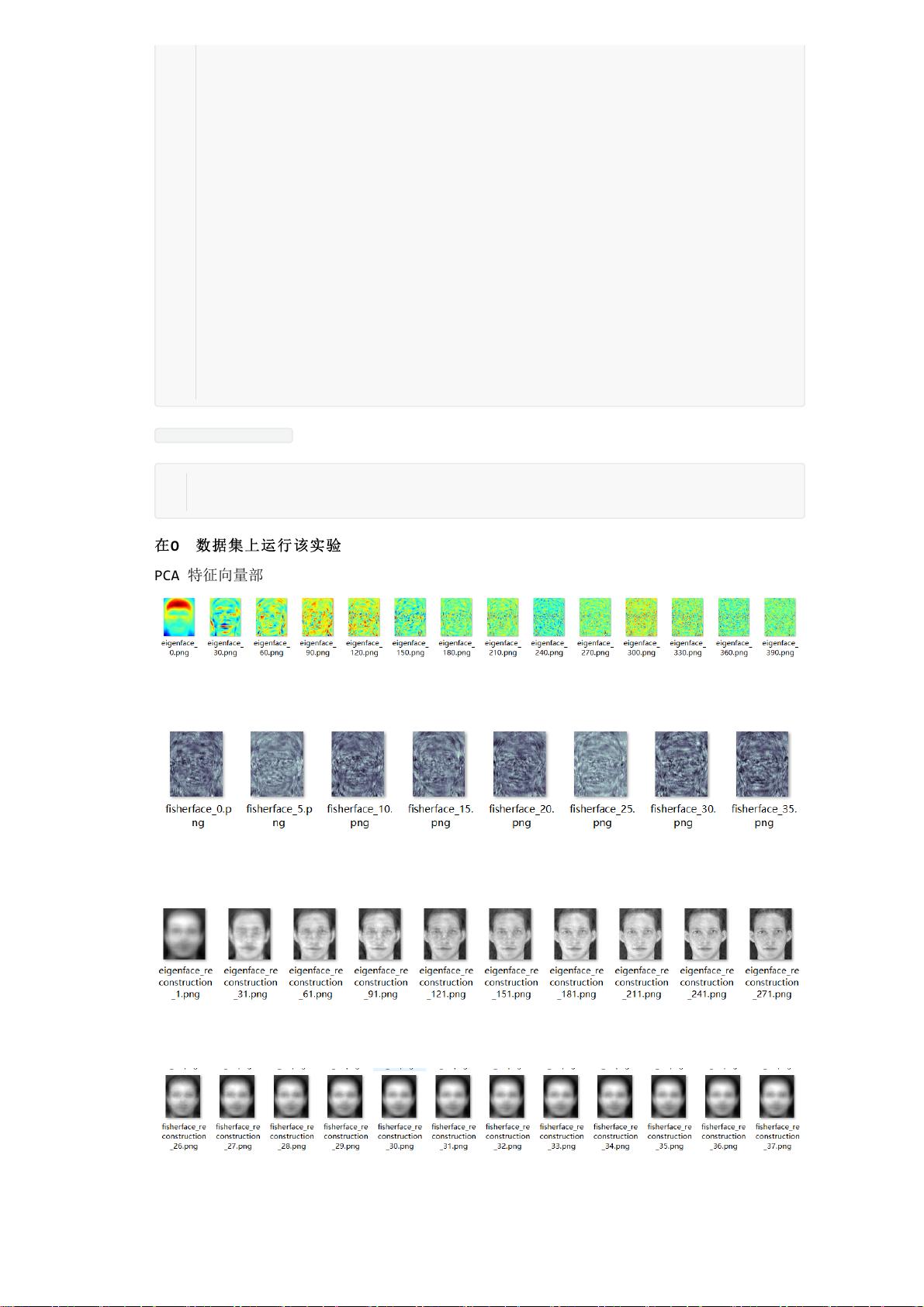
"该资源是张逸凯，一个计算机科学与技术系的本科生的学习资料，主要涉及矩阵范数、PCA人脸识别、SVM、概率分布、距离度量学习等多个IT领域的知识点。具体包括矩阵条件数的概念及其对解稳定性的影响，PCA（主成分分析）在人脸识别中的应用，以及使用LIBSVM和LIBLINEAR库进行支持向量机和线性分类的实践。" 在IT领域，矩阵范数是一个重要的数学概念，它在数值线性代数中用于衡量矩阵的“大小”或“强度”。矩阵条件数是矩阵范数的一个关键属性，用于分析矩阵求逆或解线性方程组时的稳定性。当矩阵的条件数很大时，这意味着矩阵接近于奇异，解对输入数据的微小变化非常敏感，可能导致计算结果的显著变化。在实际应用中，了解矩阵条件数有助于选择合适的算法或预处理步骤来改善计算的稳定性。 PCA（主成分分析）是一种常见的降维技术，在人脸识别中起到关键作用。ORL人脸数据库是一个经典的数据集，包含40个人的10张不同表情和光照条件下的灰度图像。通过PCA，可以提取图像的主要特征，减少数据维度同时保留大部分信息，从而实现人脸识别。在PCA中，创建EigenFace识别器并训练模型，可以获取特征向量和特征值，这些信息对于理解和优化人脸识别过程至关重要。 此外，资料还提及了SVM（支持向量机）和LIBSVM库，这是一个强大的工具，用于构建分类和回归模型。SVM通过找到最优超平面最大化类别间隔，能够处理非线性数据。LIBLINEAR则是一个用于线性分类的库，其效率高且适用于大规模数据集。 概率分布如帕累托分布是统计学中的概念，常用于描述在某些问题中少数事件占据主导的情况。在机器学习中，这种分布可能用于建模异常检测或风险分析。 最后，资源还讨论了距离度量学习，如LIBLINEAR库中的实现，这在机器学习中用于评估样本之间的相似性，对分类和聚类任务至关重要。最大熵分布则是概率论中的概念，常用于寻找最不确定但又满足约束的分布，常见于自然语言处理等领域。 这份学习资料涵盖了从基础的矩阵理论到高级的机器学习算法，是深入理解计算机科学尤其是数据处理和机器学习的宝贵资源。