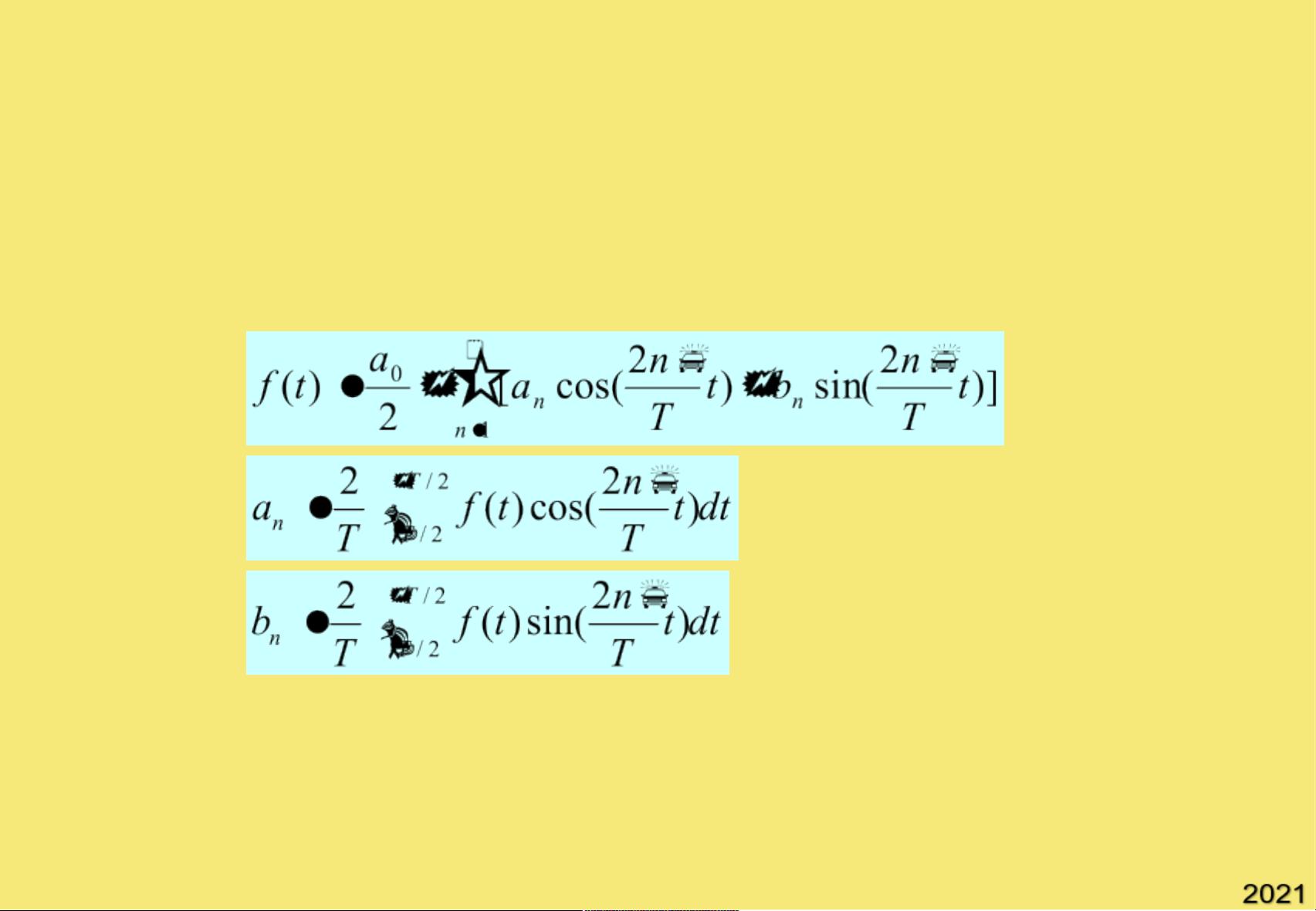"现代通信中的傅立叶变换与信号类型解析"
170 浏览量
更新于2024-01-31
1
收藏 4.79MB PPTX 举报
现代通信傅立叶变换是一种用于处理信号的数学工具,它可以将复杂的信号分解成不同频率成分的叠加。这个概念可以在现代通信中发挥重要作用,因为它可以帮助我们理解和处理各种类型的信号。
傅立叶变换涉及到周期函数、随机函数、连续-离散函数等不同的信号类型。周期函数具有重复性,可以用一个周期来描述。例如,周期函数 f(t) 可以通过 f(t) = f(t + nT) (n = 0, ±1, ±2 …)来进行表示,其中 T 是函数的周期。而随机函数则是无法通过简单的周期来描述的,它没有规律可循。而连续-离散函数则是将连续的函数转化为离散的信号,在现实世界中具有广泛应用。
典型的信号类型包括正弦函数、余弦函数、方波、阶跃信号等。这些信号在现代通信中经常出现,并且通过傅立叶变换可以将它们分解成不同频率的成分。
傅立叶变换有三种常见的数学表述方法。第一种是傅立叶级数求和表示法,其中通过给定函数形式 f(t),可以计算各级系数 an 和 bn。第二种是另一种表示法,通过一组复数形式来表示。第三种表示法是复数表示法,其中复数形式更加简洁,可以更方便地计算。
傅立叶变换的一个重要物理意义是,周期性变化的物理量可以等效为一组正弦变化的物理量分别单独作用后的线性叠加。这意味着我们可以用傅立叶变换将一个周期性方波函数表示为一系列的正弦函数的叠加。
通过理解现代通信傅立叶变换的原理和应用,我们可以更好地处理和分析不同类型的信号。这对于通信工程师和信号处理领域的科研人员来说是非常重要的。傅立叶变换的发展和广泛应用,为我们在通信领域取得了巨大的进步,也为我们理解和掌握信号处理技术提供了有力的工具。
总之,现代通信傅立叶变换是一种重要的数学工具,它可以将复杂的信号分解成不同频率成分的叠加。它涉及到周期函数、随机函数、连续-离散函数等不同的信号类型,可以通过不同的数学表述方法进行表示。通过理解和应用傅立叶变换,我们可以更好地处理和分析不同类型的信号,为现代通信领域的发展和技术创新提供有力支持。
2022-11-16 上传
2022-11-13 上传
2021-10-11 上传
2021-09-23 上传
2021-09-25 上传
2021-09-22 上传
2021-09-24 上传
xinkai1688
- 粉丝: 379
- 资源: 8万+
最新资源
- 深入浅出:自定义 Grunt 任务的实践指南
- 网络物理突变工具的多点路径规划实现与分析
- multifeed: 实现多作者间的超核心共享与同步技术
- C++商品交易系统实习项目详细要求
- macOS系统Python模块whl包安装教程
- 掌握fullstackJS:构建React框架与快速开发应用
- React-Purify: 实现React组件纯净方法的工具介绍
- deck.js:构建现代HTML演示的JavaScript库
- nunn:现代C++17实现的机器学习库开源项目
- Python安装包 Acquisition-4.12-cp35-cp35m-win_amd64.whl.zip 使用说明
- Amaranthus-tuberculatus基因组分析脚本集
- Ubuntu 12.04下Realtek RTL8821AE驱动的向后移植指南
- 掌握Jest环境下的最新jsdom功能
- CAGI Toolkit:开源Asterisk PBX的AGI应用开发
- MyDropDemo: 体验QGraphicsView的拖放功能
- 远程FPGA平台上的Quartus II17.1 LCD色块闪烁现象解析