中考数学：最值问题解决策略——构造与转化

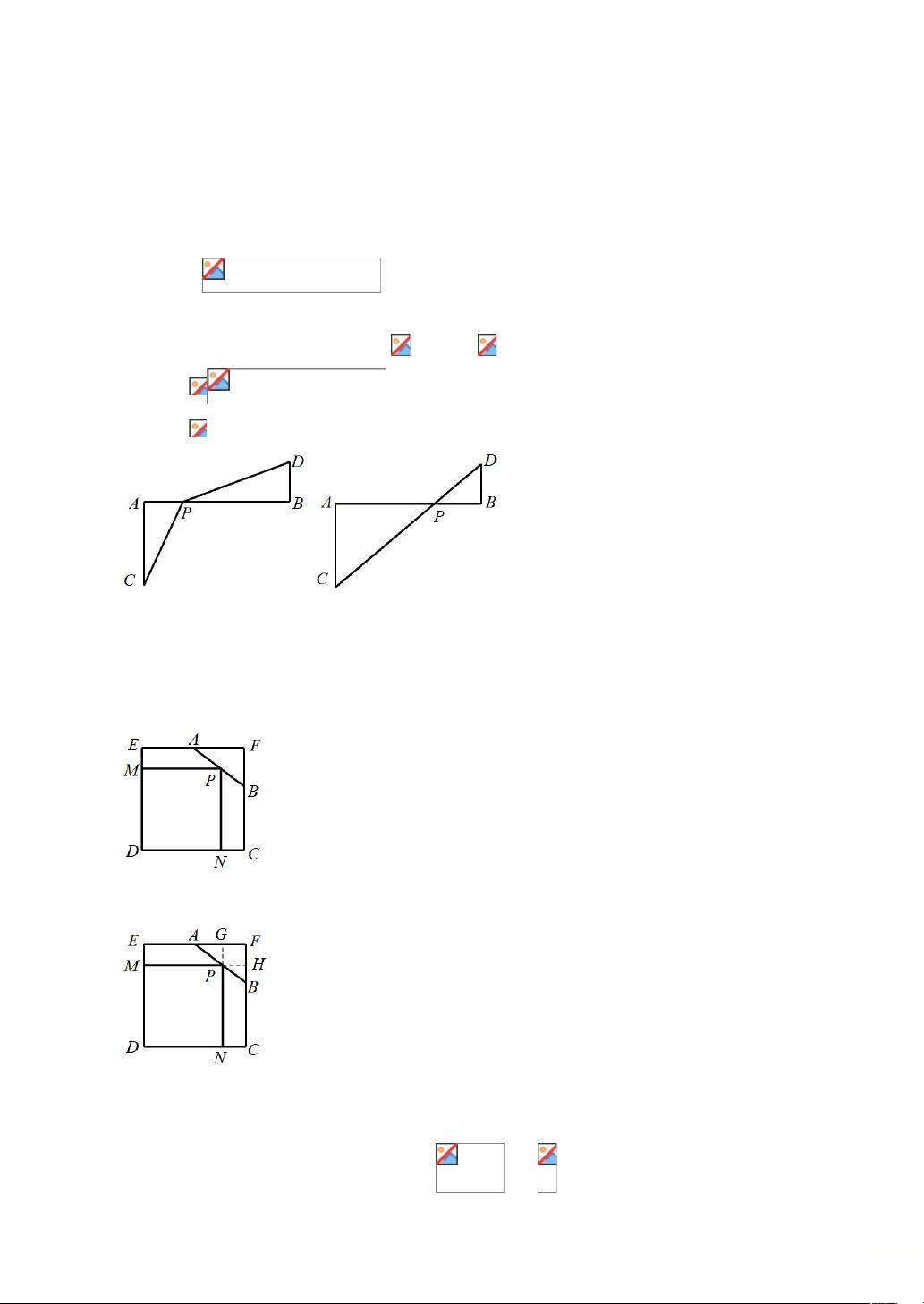
"第11讲 最值问题之构造与转化" 在中考数学培优专题中，最值问题是一项重要的考点，主要涉及如何找到某个量的最大值或最小值。本讲义详细介绍了如何通过构造和转化的方法来解决这类问题。转化是数学解题的关键技巧，分为具体转化和思维转化。具体转化通常涉及到利用数学定理和性质，将问题的条件或结论转换为更容易处理的形式。而思维转化则更注重于改变解决问题的角度和思路，对学生的抽象思维能力有较高的要求。 例题1展示了将代数问题转化为几何问题。题目中求代数表达式的最小值，通过构建几何图形，将问题转化为求线段CP+PD的最小值。利用几何性质，当C、P、D三点共线时，CP+PD的值达到最小，即为线段CD的长度。 例题2则是将几何问题转化为代数问题。在正方形CDEF中，通过设立未知数x表示PM和PN的长度，构建函数表达式，然后利用相似三角形的性质找出PM和PN的关系，最终通过求解函数的最大值来确定四边形PMDN面积的最大值。 例题3是通过构造双子型进行转化。在等腰直角三角形MBC中，利用圆的性质和等腰直角三角形的相似性，将AC的长度转化为点M在圆上的运动轨迹问题，从而找到AC长度的取值范围。 例题4同样是在直角三角形中寻找长度的最值，这次是通过作辅助线PM来解决。在Rt△ABC中，通过对点P的移动，分析CP的长度变化，从而确定AC长度的变化范围。 解决最值问题的关键在于灵活运用转化思想，结合代数和几何的方法，将复杂问题简化。这需要学生具备扎实的数学基础知识，同时能跳出常规思维，善于从不同角度审视问题。在备考过程中，通过大量练习和理解这些转化技巧，可以有效提高解题效率和准确性。