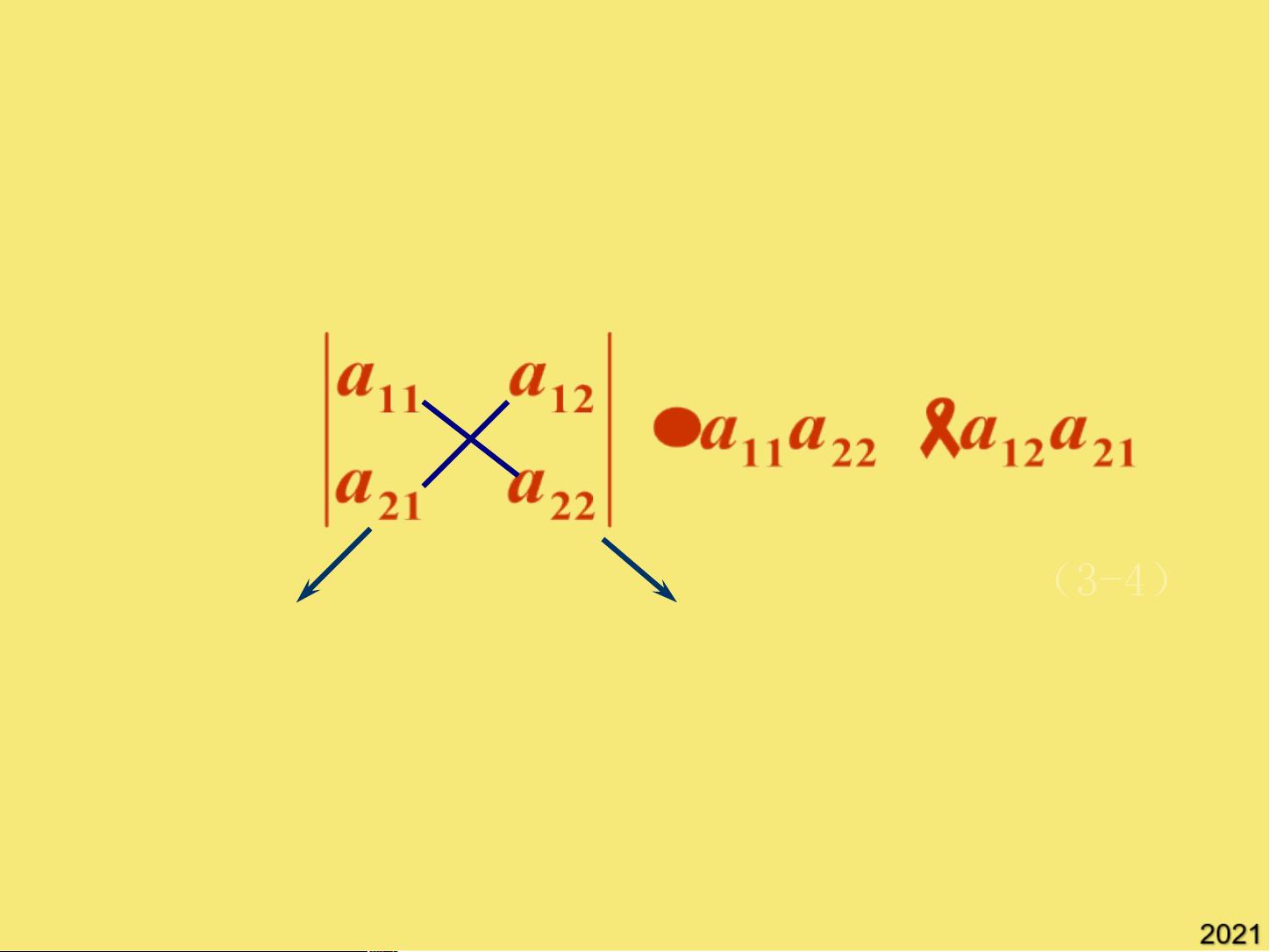单片机原理：行列式计算与n阶矩阵应用详解

单片机原理与应用的第三章和第四章专注于矩阵和行列式的理论及其在单片机中的应用。这些46页的PPT文档详细介绍了行列式的概念和计算方法，从基础的n阶行列式的定义开始，强调了行列式值的确定并不严格依赖于具体的元素顺序，而是通过特定的计算规则得到的。一阶行列式的值就是矩阵的唯一元素，二阶行列式的值则可以通过交叉相乘并取符号的方式来计算，如例1和例2所示。 对于二阶和三阶行列式，分别展示了它们的计算公式，以及如何通过实线虚线的划分来确定元素的正负号。进一步推广到n阶行列式，其值是由n个元素的乘积组成的多项式，包含n!个不同的项，这些项由排列组合决定，且与矩阵元素的位置相关。 在处理更高阶的行列式时，比如四阶以上，讲解了如何进行求解，尽管随着阶数增加，计算复杂度提高，但关键在于理解行展开定理，它允许将行列式按照任意一行或者一列展开计算。另外，还涉及到了行列式的性质，如转置不改变行列式的值，数乘行列式的结果是原行列式的数倍，以及加法和逆运算对行列式的影响。 章节中也讨论了特殊的行列式形式，如上三角行列式和下三角行列式，这些特殊情况下的行列式求解可能会简化计算过程。例如，上三角行列式只依赖于对角线上的元素，而下三角行列式的求解可以利用这个特点。至于初等变换，它们如何影响行列式，也是学习的重点，因为行列式的值在矩阵经过行或列的交换、缩放、移位等基本变换后可能发生变化。 这部分内容深入浅出地讲解了单片机应用中矩阵和行列式的概念、计算方法以及它们在处理线性方程组、特征值问题等实际问题中的作用，是理解和掌握单片机原理与应用的关键部分。