MatlabPDE工具箱：有限元法求解偏微分方程详解

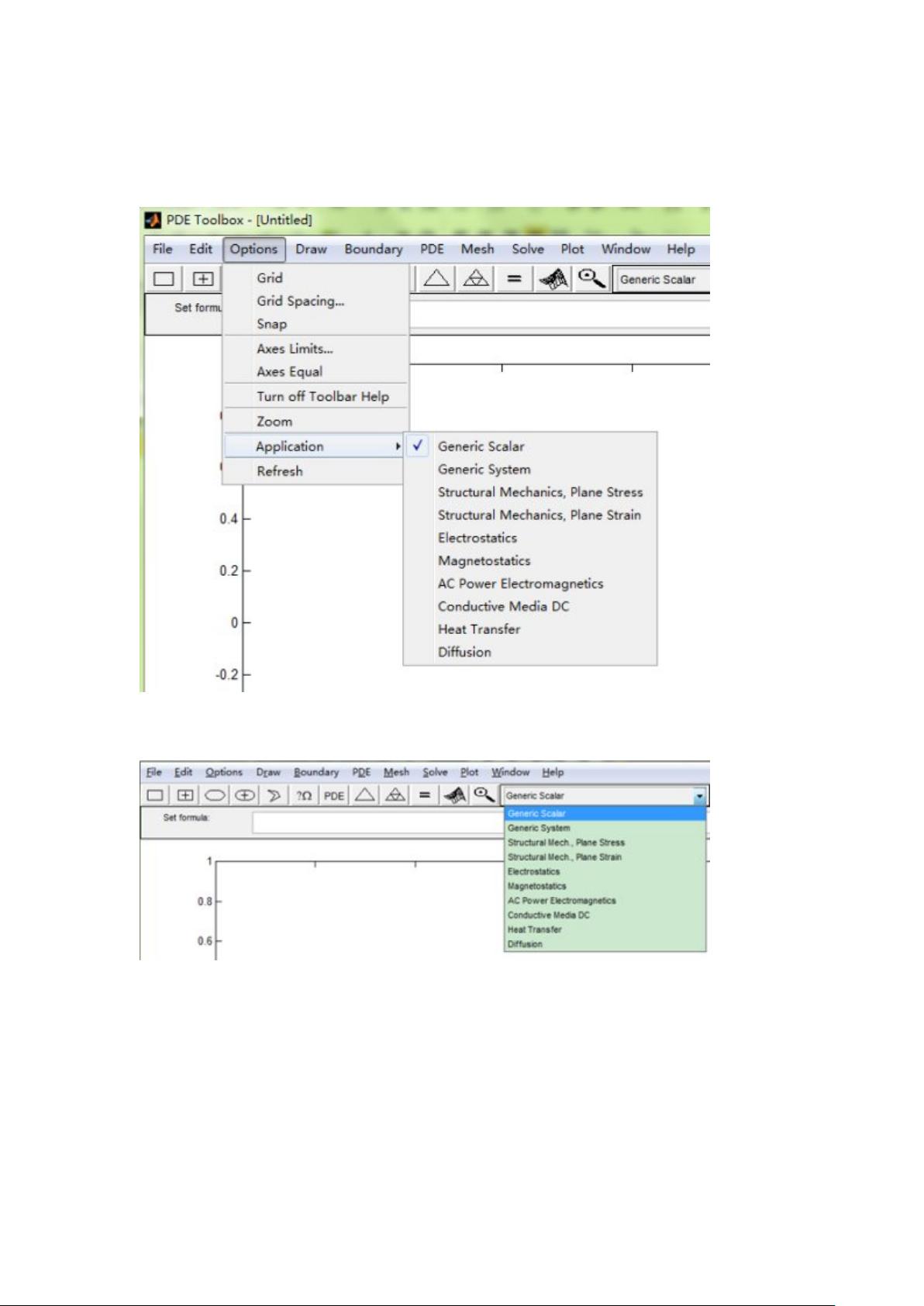
"MatlabPDE工具箱是一个用于求解偏微分方程(PDE)的数值计算工具，它利用有限元法进行数值求解。该工具箱提供了一个直观的图形用户界面，允许用户通过一系列步骤来解决各种科学和工程问题，如结构力学、电磁学、热传导和扩散等。在Matlab环境中，通过输入`pdetool`可以启动PDE工具箱。" 在实际应用中，解决偏微分方程通常涉及以下关键步骤： 1) **建立几何模型**：首先，用户需要定义问题所涉及的几何区域，这可以通过绘制或导入几何形状来完成。PDE工具箱支持多种几何形状的创建，以便模拟实际问题的复杂结构。 2) **定义边界条件**：边界条件是PDE问题的重要组成部分，它们描述了问题区域边缘上的物理特性。用户可以在工具箱的界面上指定不同的边界条件，例如固定边界、滑移边界或特定的边界值。 3) **定义PDE类型和系数**：用户需要确定要解决的偏微分方程类型（如拉普拉斯方程、热传导方程等）并输入相关的系数。PDE工具箱支持多种类型的线性和非线性PDE，可以根据问题的具体性质进行选择。 4) **三角形网格划分**：为了将连续的几何区域转化为离散的数值问题，工具箱会自动生成或允许用户手动创建三角形网格。网格的质量对求解的精度有直接影响，因此网格划分是至关重要的一步。 5) **有限元求解**：在定义好网格后，工具箱会利用有限元方法将PDE离散化，转化为一组线性代数方程组。然后，Matlab的内置求解器会求解这个方程组，给出数值解。 6) **解的图形表达**：求解完成后，结果可以通过图形化方式展示，用户可以观察解的分布和特性，进一步分析和理解问题的结果。 在PDE工具箱中，用户可以选择不同的应用模式以适应不同领域的具体问题，例如结构力学、电磁学、热传导等。此外，通过全局设置，用户还可以调整网格显示、坐标轴限制以及其他可视化选项，以优化模型的显示效果。 对于更复杂的问题，Matlab的PDE工具箱可能不足以满足所有需求，这时可以考虑使用像COMSOL Multiphysics这样的专业多物理场软件，它提供了更高级的建模和求解能力。 MatlabPDE工具箱是解决偏微分方程数值问题的强大工具，尤其适合教学和研究环境中的初学者以及需要快速原型验证的工程师。通过熟练掌握其操作，用户能够有效地处理各种科学和工程领域的PDE问题。