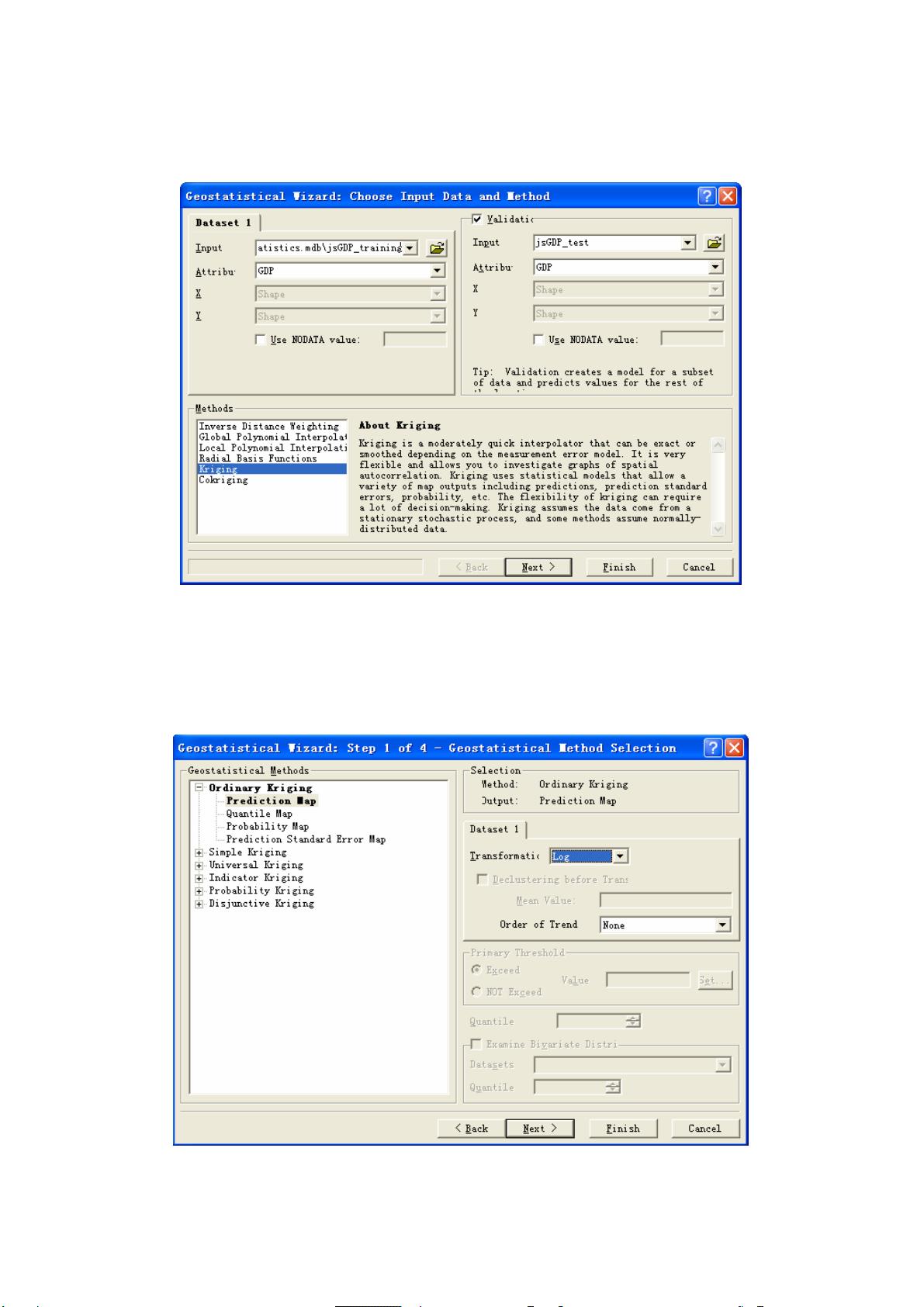
克里格插值法详解与应用条件

"地统计插值方法是一种在地理信息系统（GIS）中广泛使用的空间数据分析技术，主要用于估计在未采样地点的数值。其中，克里格插值是地统计学的核心方法，它基于空间自相关性的理论，通过分析数据的半方差函数来构建插值模型，提供无偏的估计。在克里格插值中，数据的质量、数量以及合适的参数选择至关重要。例如，数据应该满足一定的前提假设，通常要求数据点足够多，且分布均匀。在实际操作中，需要调整的参数包括块金值、基台值、变程和拟合函数，这些参数会直接影响到插值结果的准确性。 克里格方法有多种变体，如普通克里格、简单克里格、泛克里格、协同克里格、对数正态克里格和析取克里格等。在选择合适的克里格方法时，需要根据数据的特性和应用场景来决定。例如，如果数据服从正态分布，可以使用对数正态克里格；数据存在明显的趋势，则适合使用泛克里格；对于属性值是否超过特定阈值的问题，指示克里格较为适用；而在两种属性间存在相关性的情况下，协同克里格能有效地进行插值。 以ArcGIS软件为例，普通克里格插值是其中的基础应用，适用于期望值未知且数据呈正态分布的情况。这一方法的流程包括创建预测图、变异函数模型、预测和标准误差地图的生成。在实施普通克里格插值时，用户需要选择合适的变程和拟合函数，以最优化模型。泛克里格则允许考虑空间趋势，适用于数据具有线性或非线性趋势的场景。而协同克里格则在两种或多种属性相关时，利用一种属性来帮助预测另一种属性的空间分布。 在执行克里格插值时，需要注意数据预处理、模型验证和结果解释等环节。数据预处理包括数据清洗、缺失值处理和异常值检测。模型验证则通过比较插值结果与实际观测值的差异，如残差分析和交叉验证，以评估模型的可靠性。最后，对插值结果的解释应当结合地理背景和专业知识，理解空间模式的意义和潜在的不确定性。 地统计插值，尤其是克里格方法，是GIS中解决空间数据不完整性问题的重要工具。它通过科学的统计方法和参数调整，能够提供对未知区域的数值预测，为环境科学、地质学、气象学等多个领域提供了有力的数据支持。"