马尔可夫矩阵与傅里叶级数浅析

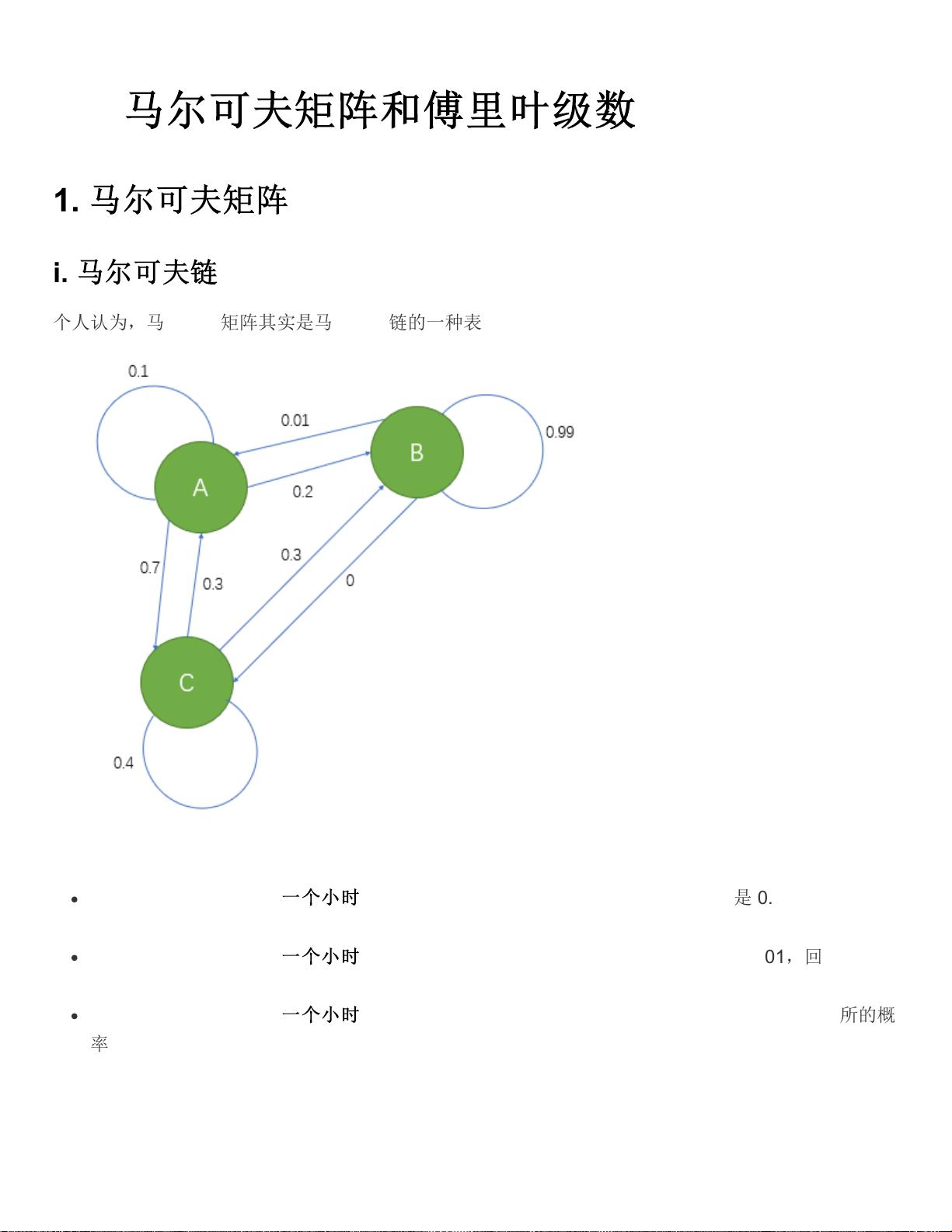
"这篇内容介绍了马尔可夫矩阵和它在描述随机过程中的应用，特别是与马尔可夫链的关联。文章通过一个简单的家庭房间转换的例子解释了马尔可夫矩阵的概念，强调了马尔可夫过程的关键特性，如无后效性、可达性以及无周期性。同时，讨论了马尔可夫矩阵的幂仍然是马尔可夫矩阵的性质，以及如何寻找马尔可夫矩阵的稳态，即平衡状态。" 马尔可夫矩阵，也称为转移矩阵，是用于描述马尔可夫链的一个工具。马尔可夫链是一种数学模型，其中系统状态的未来变化只依赖于当前状态，而不依赖于它是如何达到当前状态的历史路径。在这个例子中，三个房间代表了三个可能的状态，每个房间的转移概率构成了马尔可夫矩阵。 矩阵A如下所示： \[ A = \begin{bmatrix} 0.1 & 0.2 & 0.7 \\ 0.01 & 0.99 & 0 \\ 0.3 & 0.3 & 0.4 \end{bmatrix} \] 每个元素\( A_{ij} \)表示从状态i转移到状态j的概率。矩阵的行和列分别对应起始和结束状态。马尔可夫矩阵具有非负元素（因为概率不能为负）和归一化性质（每一行的元素之和为1，表示从任一状态出发，总概率为1）。 马尔可夫矩阵的幂仍为马尔可夫矩阵，这是因为每次幂运算保留了非负性和归一性的特性。随着幂指数的增加，矩阵趋向于稳定，即达到一种平衡状态，此时所有状态的转移概率保持不变，即找到了稳态分布。稳态分布满足以下条件： \[ \pi P = \pi \] 其中，\( \pi \)是稳态分布向量，P是马尔可夫矩阵。这意味着在长期趋势下，系统会以某种固定的比例停留在各个状态。 寻找马尔可夫矩阵的稳态可以通过求解特征值问题来实现，即找到矩阵P的特征值和对应的特征向量。如果存在一个特征值为1，那么对应的特征向量就是稳态分布。其他所有特征值应为负数，以确保系统的收敛性。 在实际应用中，马尔可夫矩阵和马尔可夫链广泛应用于各种领域，如天气预报、语言建模、生物学的种群动态分析、经济预测等，帮助我们理解和预测那些具有马尔可夫性质的复杂系统的行为。