MATLAB实现抽样定理仿真分析

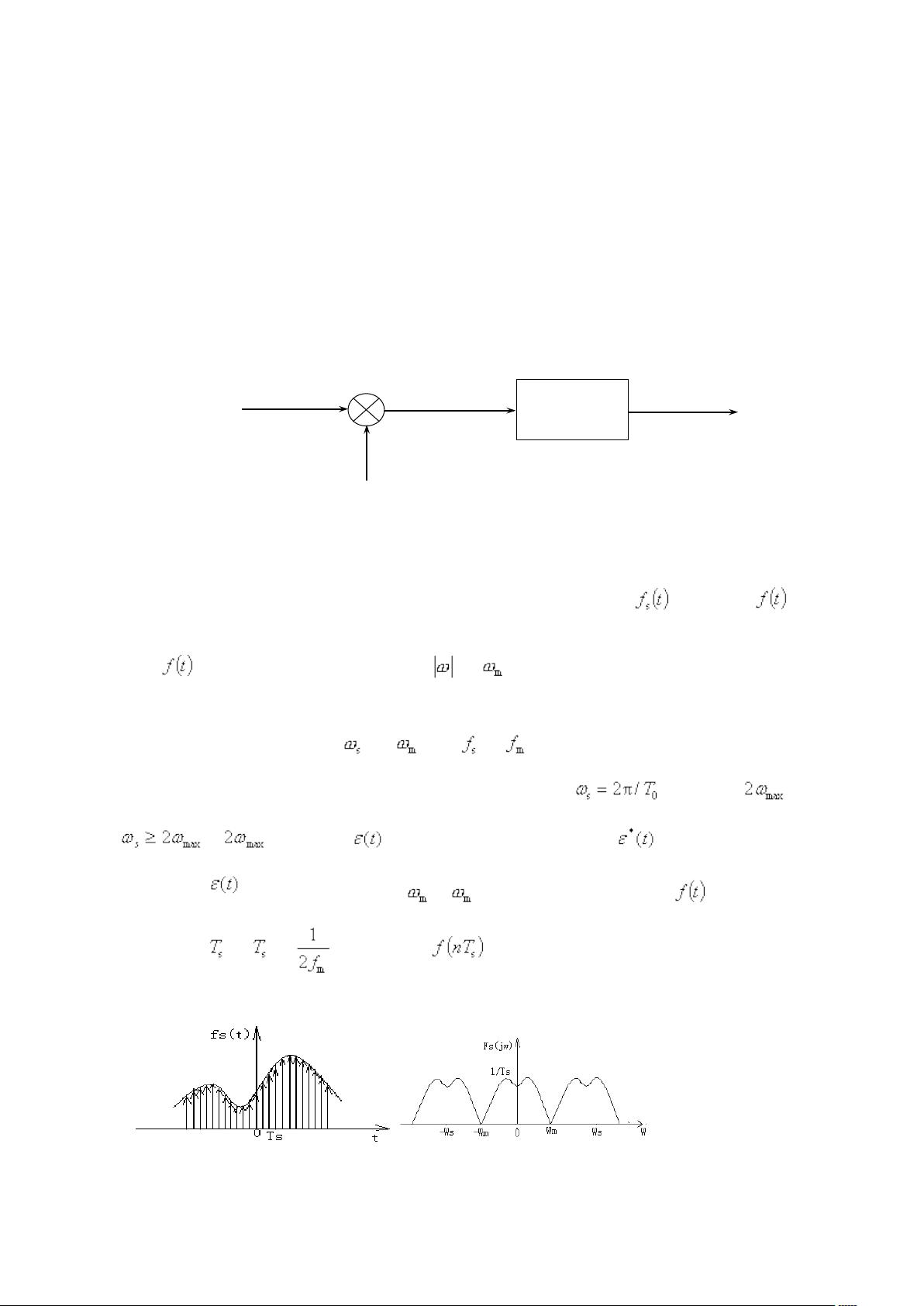
"本文档主要探讨了如何利用MATLAB来实现抽样定理，并通过仿真来研究过抽样和欠抽样的效果以及恢复系统的性能。内容包括抽样定理的理论基础，信号采样的原理，以及不同抽样频率下信号频谱的变化情况。" 在信号处理领域，抽样定理是至关重要的概念，它规定了为了从模拟信号无失真地恢复数字信号，所需的最低采样频率。这个定理指出，如果一个信号是带限的，即它的频谱在某个特定频率之外为零，那么采样频率必须至少是该信号最高频率成分的两倍。这个频率被称为奈奎斯特定理的采样频率，通常表示为fs。如果采样频率低于这个阈值，就会发生混叠现象，导致信号失真。 MATLAB作为一种强大的计算工具，被广泛用于信号处理和模拟。在这个课程设计中，作者使用MATLAB来构建和仿真模拟信号的抽样与恢复系统。通过改变抽样频率，可以观察到当抽样频率过高、适中或过低时，信号频谱的变化。例如，当抽样频率fs足够高时（如图2.1(b)所示），信号频谱不会发生混叠，可以准确恢复原始信号；而当抽样频率过低（如图2.1(c)所示）时，频谱会发生混叠，恢复出的信号会失真。 在信号采样的过程中，通常使用脉冲序列来对模拟信号进行采样。如图1所示的原理图，模拟信号x(t)通过一个理想的冲激采样函数δ(t)进行采样，得到采样信号x[n]。采样函数的傅立叶变换是其自身的复制，而被采样信号的傅立叶变换与采样函数的傅立叶变换进行卷积，结果就是采样信号的频谱。如果信号x(t)的带宽为B，且采样频率fs > 2B，那么采样后的频谱会保持原信号的频谱特性，避免混叠。 在实际应用中，理解并正确运用抽样定理至关重要，因为它直接影响着信号的传输质量和数据的准确性。MATLAB的仿真功能使我们能够直观地看到理论与实践的结合，帮助我们更好地理解和掌握抽样定理的实际应用。通过这种仿真方法，不仅可以验证抽样定理的正确性，还可以研究不同采样策略对信号质量的影响，对于理解和优化通信系统、音频处理、图像处理等各种领域的信号处理过程有着积极的作用。