回溯策略详解：从货郎问题到算法应用

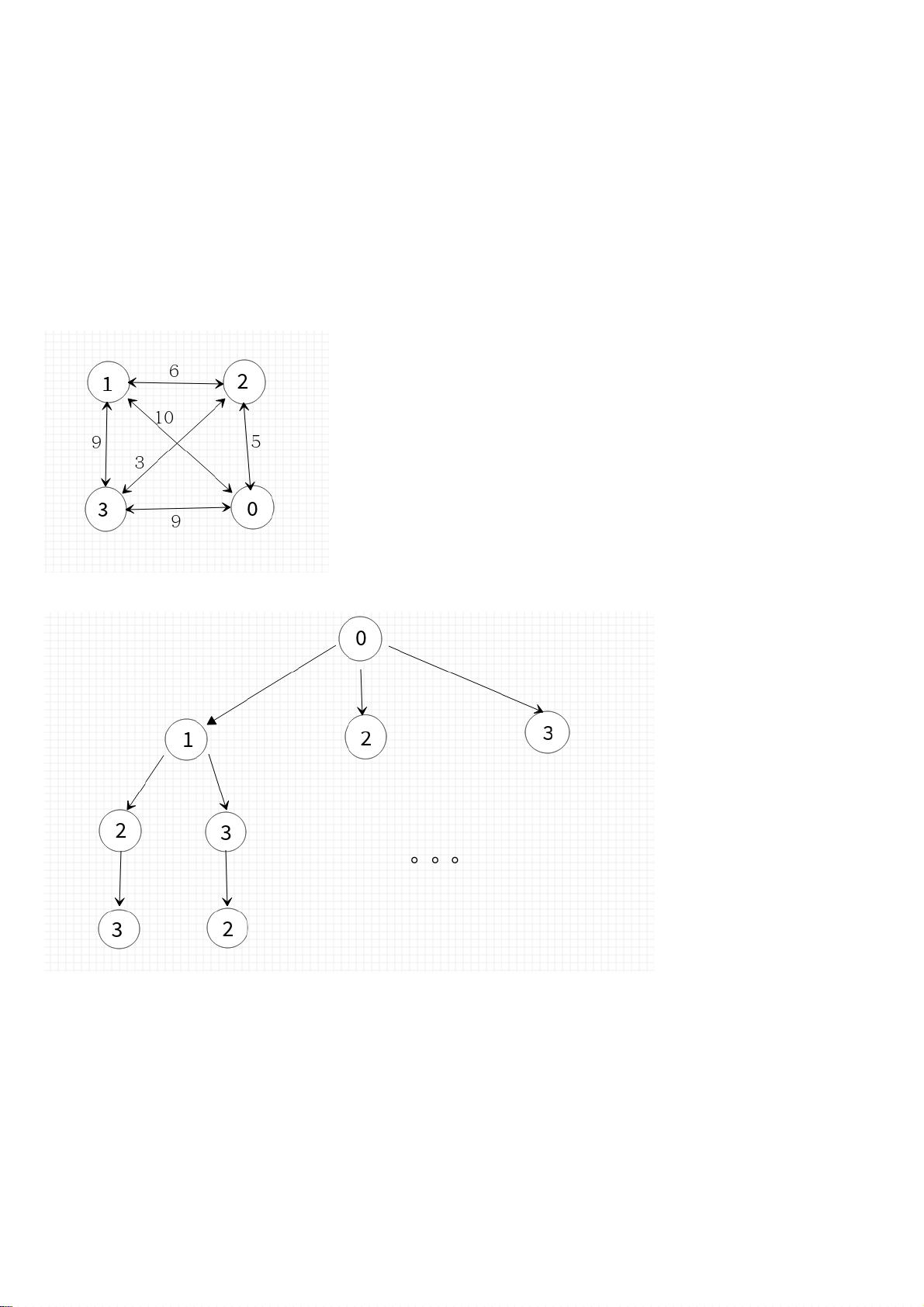
"本文主要介绍了五大常见算法策略之一的回溯策略，并以货郎问题为例进行详细阐述。回溯策略是一种基于树形结构的解空间搜索方法，通过尝试不同的路径来寻找满足条件的解，当发现当前路径无法满足条件时，会回溯到上一步寻找其他可能性。货郎问题要求找到一个无向带权图中最短的包含所有城市的环路，通过深度优先搜索和回溯策略可以解决这一问题。" 回溯策略是一种在解决问题时采用试探性的方法，当发现当前选择无法达到目标时，会撤销之前的决定，尝试其他可能的选择，以寻找满足条件的解决方案。这种策略通常用于解决组合优化问题，如旅行商问题、八皇后问题等。在回溯策略中，解空间往往被表示为一棵树，从根节点到叶节点的路径对应于一个可能的解。 货郎问题是一个经典的回溯策略应用实例。给定一个无向带权图，货郎需要找到一个经过所有城市的最短路径，最后返回起点。这个问题可以通过构建一个解空间树，然后进行深度优先搜索来解决。在搜索过程中，每次选择一个未访问过的相邻城市，直到所有城市都已被访问过。如果在某次选择后发现无法找到满足条件的路径，就回溯到上一步，尝试选择其他相邻城市。 文章中给出了一个简单的货郎问题实例，包括4个城市和它们之间的距离。为了解决这个问题，定义了一个二维数组`map`来存储城市间的距离，并使用`city`数组记录每个城市是否被访问过，`road`数组存储路径。通过递归函数`travel`实现回溯搜索，参数包括当前城市的访问状态、上一个访问的城市、当前路径的总长度以及当前所在的城市位置。当到达最后一个城市时，检查当前路径长度是否小于已知的最短路径，如果是，则更新最短路径。 在实际的`travel`函数中，每次递归调用都会尝试访问下一个未访问的城市，如果所有城市都被访问过，就比较当前路径的长度，然后回溯。回溯是通过改变`city`和`road`数组的状态实现的，撤销之前的选择，尝试不同的路径。 总结来说，回溯策略是解决复杂问题的一种有效方法，它通过探索解空间的分支来寻找符合条件的解。在货郎问题中，利用深度优先搜索结合回溯策略，可以找到最短的环路路径。理解并掌握回溯算法对于解决实际的组合优化问题至关重要。