量子场论中的复杂性对称性：芬斯勒几何与薛定谔方程新解
95 浏览量
更新于2024-07-16
收藏 1017KB PDF 举报
本文主要探讨了量子场论中复杂性的原理及其对称性，该研究基于离散电路复杂性的概念，扩展到了连续系统的复杂性分析。作者首先强调了芬斯勒度量在连续系统复杂性几何中的自然出现，它是描述系统动态行为的一种关键工具。芬斯勒度量在此背景下具有特殊意义，因为量子场论的基本对称性导致它受到额外的约束，特别是SU(n)算子的复杂度与Finsler几何中的测地线长度有直接关联。
在这个理论框架下，Finsler度量表现出双不变性，这与离散qubit系统中的右不变性形成鲜明对比。双不变性在量子场论中扮演着关键角色，因为它确保了理论的对称性和一致性。通过将连续系统与离散qubit系统进行比较，研究者揭示了这种双不变性在不同层次上的通用性，许多离散系统中的局部不变性质同样能在连续系统中找到对应。
作者还提出了一个新观点，即在孤立系统中，薛定谔方程的演化可以解释为量子态通过最小化“计算成本”（即复杂度）的过程。这种解释建立在形式主义的双不变性基础上，提供了一个深刻理解量子系统动力学的新视角。这一研究成果发表在《欧洲物理杂志C》上，是开放获取的，便于学术界同仁进一步研究和讨论。
总结来说，这篇文章深入研究了量子场论中的复杂性概念，展示了其与芬斯勒度量、对称性以及薛定谔方程之间的内在联系，为理解量子系统的动态行为提供了新的理论工具。它不仅丰富了量子复杂性理论的理论基础，也为量子信息科学和技术领域的未来发展提供了有价值的方向。
109 Page 4 of 20 Eur. Phys. J. C (2019) 79 :109
(
ˆ
O
1
ˆ
O
2
)|ψ:=
ˆ
O
1
(
ˆ
O
2
|ψ), ∀|ψ . (2.4)
By the definition of realizable operators, it can be shown that
ˆ
O
1
ˆ
O
2
is realizable if
ˆ
O
1
and
ˆ
O
2
are both realizable operators.
Thus, O forms a monoid (semigroup with identity).
If we restrict physical processes to quantum mechanical
processes, Eq. (2.1) implies that realizable operators are all
unitary rather than Hermitian. In other words, our target is a
property of the physical process rather than a direct observ-
able. As quantum circuits are quantum mechanical processes
and Solovay–Kitaev theorem [31] says that all the unitary
operators can be approximated by some quantum circuits
with any nonzero tolerance, we can conclude that the realiz-
able operators set is the set of unitary operators. As unitary
operators are invertible, the realizable operators set O forms
a (finite dimensional or infinite dimensional) unitary group.
2
2.2 Definitions and axioms
Intuitively speaking, the circuit complexity (or computa-
tional complexity) of a target operator ( or computational
task) is defined by the minimal number of required funda-
mental gates ( or fundamental steps) to simulate the target
operator ( or finish the computational task). Based on this
intuitive concept of the complexity in quantum circuits and
computations, we propose that the complexity defined in
an arbitrary monoid O should satisfy the following three
axioms. We denote a complexity of an operator ˆx in an oper-
ators set O by C( ˆx).
G1 [Nonnegativity]
∀ˆx ∈ O, C( ˆx) ≥ 0 and the equality holds iff ˆx is the
identity.
G2 [Series decomposition rule (triangle inequality)]
∀ˆx, ˆy ∈ O, C( ˆx ˆy) ≤ C( ˆx) + C( ˆy).
G3 [Parallel decomposition rule]
∀( ˆx
1
, ˆx
2
) ∈ N = O
1
× O
2
⊆ O, C
( ˆx
1
, ˆx
2
)
=
C
( ˆx
1
,
ˆ
I
2
)
+ C
(
ˆ
I
1
, ˆx
2
)
.
Here, in G2, it is possible that the operator ˆx ˆy is decom-
posed in different ways, say ˆx
ˆy
. In this case, G2 can
read also as C( ˆx ˆy) = C( ˆx
ˆy
) ≤ C( ˆx
) + C( ˆy
).InG3,
we consider the case that there is a sub-monoid N ⊆ O
which can be decomposed into the Cartesian product of two
monoids, i.e., N = O
1
× O
2
.
ˆ
I
1
and
ˆ
I
2
are the identi-
ties of O
1
and O
2
. The Cartesian product of two monoids
implies that ( ˆx
1
, ˆx
2
)( ˆy
1
, ˆy
2
) = ( ˆx
1
ˆy
1
, ˆx
2
ˆy
2
) for arbitrary
( ˆx
1
, ˆx
2
), ( ˆy
1
, ˆy
2
) ∈ N .
2
Hermit operators, which correspond to observable quantities and are
not unitary in general, cannot be approximated by quantum circuits if
the tolerance is small enough.
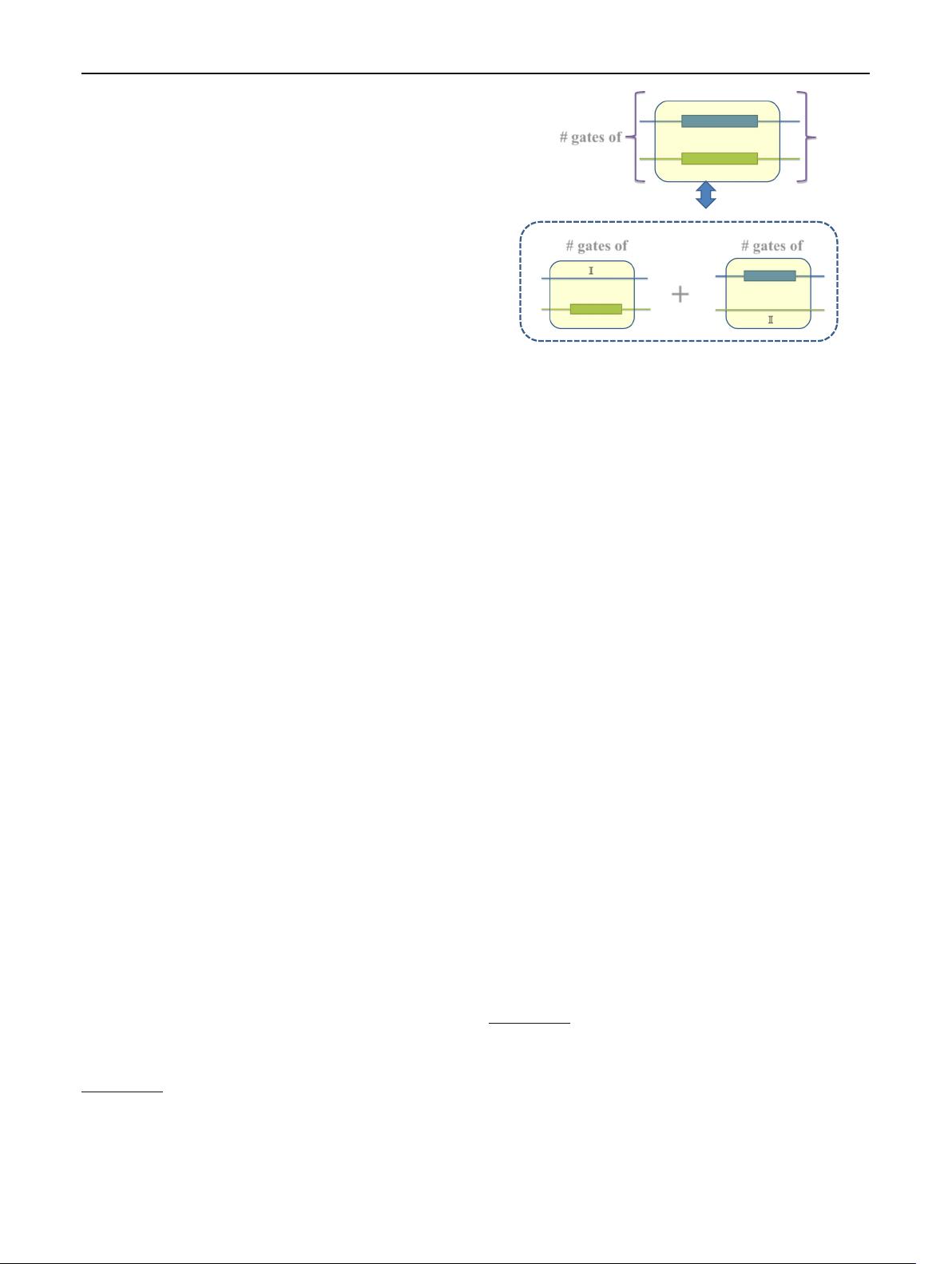
# gates of
2
ˆ
x
+
# gates of # gates of
1
ˆ
x
2
ˆ
x
1
ˆ
1
ˆ
x
2
ˆ
Fig. 2 Schematic diagram for the complexity of the Cartesian prod-
uct and parallel decomposition rule. As two operators ˆx
1
and ˆx
2
are
simulated independently, the minimally required gates for ( ˆx
1
, ˆx
2
) is
the sum of the minimally required gates for ˆx
1
and ˆx
2
.Thus,wehave
C(( ˆx
1
, ˆx
2
)) = C(( ˆx
1
,
ˆ
I
2
)) + C((
ˆ
I
1
, ˆx
2
))
The axiom G1 is obvious by definition. We call the axiom
G2 “series decomposition rule” because the decomposition
of the operator
ˆ
O =ˆx ˆy to ˆx and ˆy is similar to the decompo-
sition of a big circuit into a series of small circuits. Reversely,
the ‘product’ of two operators corresponds to a serial con-
nection of two circuits. The axiom G2 answers a basic ques-
tion: what is the relationship between the complexities of two
operators and the complexity of their products? Because the
complexity is a kind of “minimal”, we require the inequality
in G2.
3
This G2 will lead to the familiar “triangle inequality”
in the concept of distance (see F3 in the Sect. 3)soitisalso
called “triangle inequality”.
In contrast to G2 (series decomposition rule), we call the
axiom G3 “parallel decomposition rule”, which is chosen
as one of the most basic axioms in defining complexity for
the first time in this paper.
4
It comes from the following
fundamental question: if an operator (task)
ˆ
O contains two
totally independent sub-operators (sub-tasks) ˆx
1
and ˆx
2
, what
should be the relationship between the total complexity and
the complexities of two sub-operators (sub-tasks)? Here, the
totally independent means that: (a)
ˆ
O accepts two inputs and
yields two outputs through ˆx
1
and ˆx
2
, and (b) the inputs for
ˆx
1
(or ˆx
2
) will never affect the outputs of ˆx
2
(or x
1
). See Fig. 2
for this explanation.
Mathematically, the construction of a bigger operator
ˆ
O
by ˆx
1
and ˆx
2
under two requirements (a) and (b) corresponds
to the Cartesian product denoted by
ˆ
O = ( ˆx
1
, ˆx
2
). Note that
3
The reason for axiom G2 has been explained clearly also in the Niel-
son’ works [20–22].
4
In some cases, the parallel decomposition may be impossible. How-
ever, in local computations/gates, the parallel decomposition is permit-
ted, for example see Ref. [32]. Our axiom G3 does not talk about the
possibility of the parallel decomposition, but says what will happen to
the complexity if the parallel decomposition is permitted.
123
剩余19页未读，继续阅读
2019-03-11 上传
2020-05-01 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
2023-10-19 上传
2020-04-15 上传
点击了解资源详情
weixin_38697557
- 粉丝: 8
- 资源: 921
我的内容管理
展开
最新资源
- 黑板风格计算机毕业答辩PPT模板下载
- CodeSandbox实现ListView快速创建指南
- Node.js脚本实现WXR文件到Postgres数据库帖子导入
- 清新简约创意三角毕业论文答辩PPT模板
- DISCORD-JS-CRUD：提升 Discord 机器人开发体验
- Node.js v4.3.2版本Linux ARM64平台运行时环境发布
- SQLight：C++11编写的轻量级MySQL客户端
- 计算机专业毕业论文答辩PPT模板
- Wireshark网络抓包工具的使用与数据包解析
- Wild Match Map: JavaScript中实现通配符映射与事件绑定
- 毕业答辩利器：蝶恋花毕业设计PPT模板
- Node.js深度解析：高性能Web服务器与实时应用构建
- 掌握深度图技术：游戏开发中的绚丽应用案例
- Dart语言的HTTP扩展包功能详解
- MoonMaker: 投资组合加固神器，助力$GME投资者登月
- 计算机毕业设计答辩PPT模板下载
