11
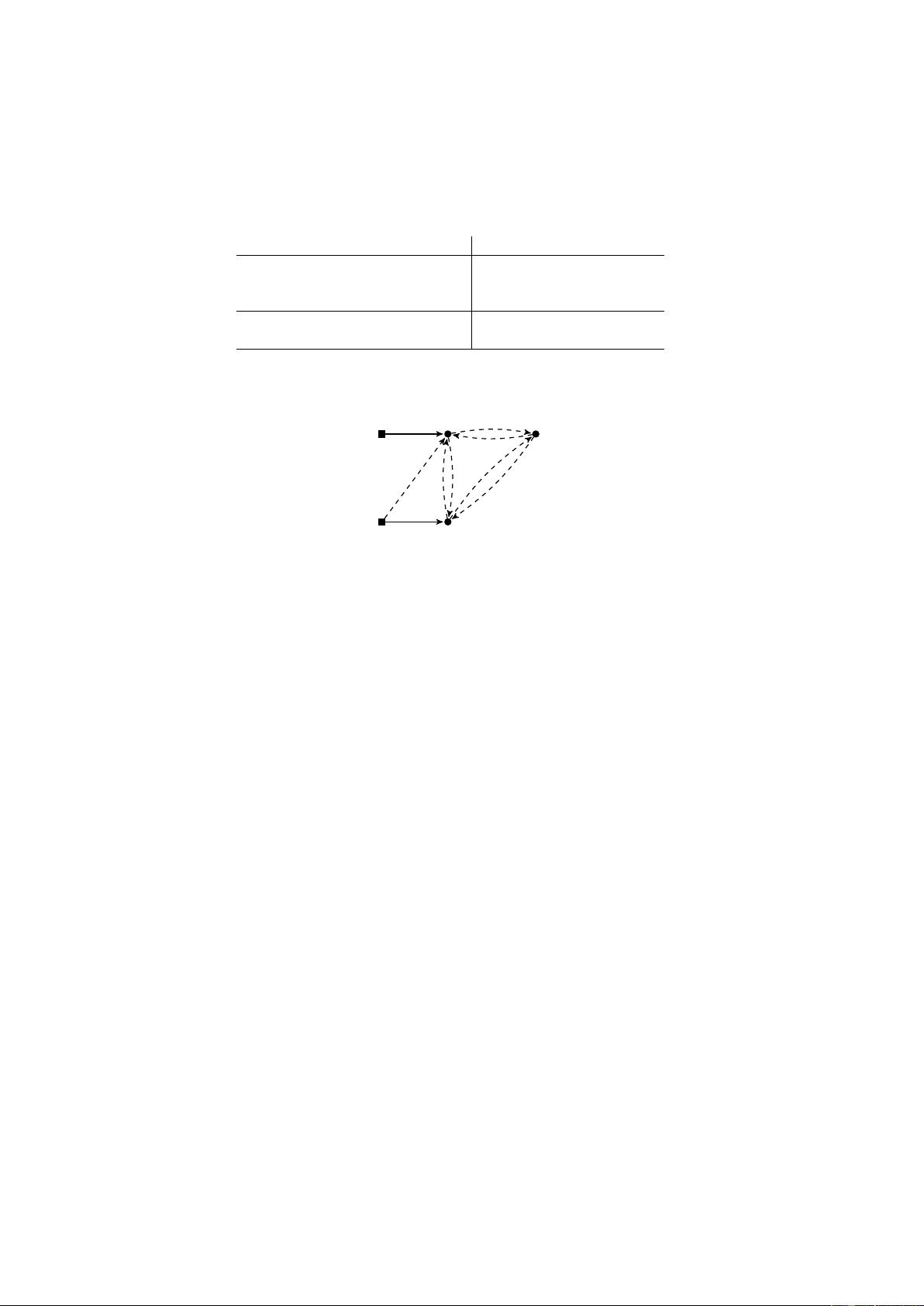
To draw the partial moral graph, moralize and disorient any causal representation of model (7) in Figure
5a or 5b. Alternatively, draw the vertices, which are the random variables of the structural model, and for
each equation add the clique of the variables included into this equation, where a clique is defined as a set
of pairwise adjacent nodes. In model (7), for example, equation (7a) includes variables p, q, and z
d
, so it
produces clique {p, q, z
d
} in the partial moral graph in Figure 5c, and equation (7b) includes p, q, and z
s
,
producing clique {p, q, z
s
}.
The algorithm of testable identification proposed in the previous example does not produce any testable
exclusion restriction here, so I use a different approach. Consider the clique cover problem for the partial
moral graph. The clique cover problem for an undirected graph is to find as few cliques as possible to cover
the entire graph. For a model with n equations, if the clique cover problem has a unique solution with n
cliques, then each clique is associated with a structural equation in such way that the variables included
into the clique are included into this structural equation, and the variables included into the equation are
included into the clique. For the moral graph depicted in 5c, the unique solution for the clique cover problem
is {z
d
, q, p} and {z
s
, q, p}. I can learn asymptotically the true moral graph from data in almost all parameter
points, and having solved the clique cover problem for the estimated moral graph, I can conclude which
variables are present in each equation. In this example, this suffices for the full testable identification.
To estimate the moral graph in Figure 5c, I need to test the hypothesis that two instruments, z
d
and z
s
,
are not adjacent in this graph. Unlike in the previous example, I cannot use conventional partial correlations
to test this hypothesis, because they can be used only for pairs of variables, where at least one variable is
endogenous. In Section 4.1, I introduce a new kind of partial correlations, referred to hereafter as conditional
partial correlations, and these correlations can also be applied to pairs of instruments. This is how I can
test the hypothesis that z
d
and z
s
are not adjacent in the conditional moral graph.
In contrast to directly testable exclusions considered in the example in Section 2.1, the exclusion con-
sidered in this section is an indirectly testable exclusion. By definition, indirectly testable exclusions are
associated with the tests of null hypotheses that there is no moralization effect between instruments. As I
discuss in Section 6, indirect tests may require stronger instruments than direct tests.
3. A Graphical Method of Identification
In this section, I formulate and prove various sufficient conditions for identification, which I have already
applied in the previous section. Consider the following simultaneous equations model (SEM):
(8) AY = BZ + E