回归分析：从一元到多元线性预测

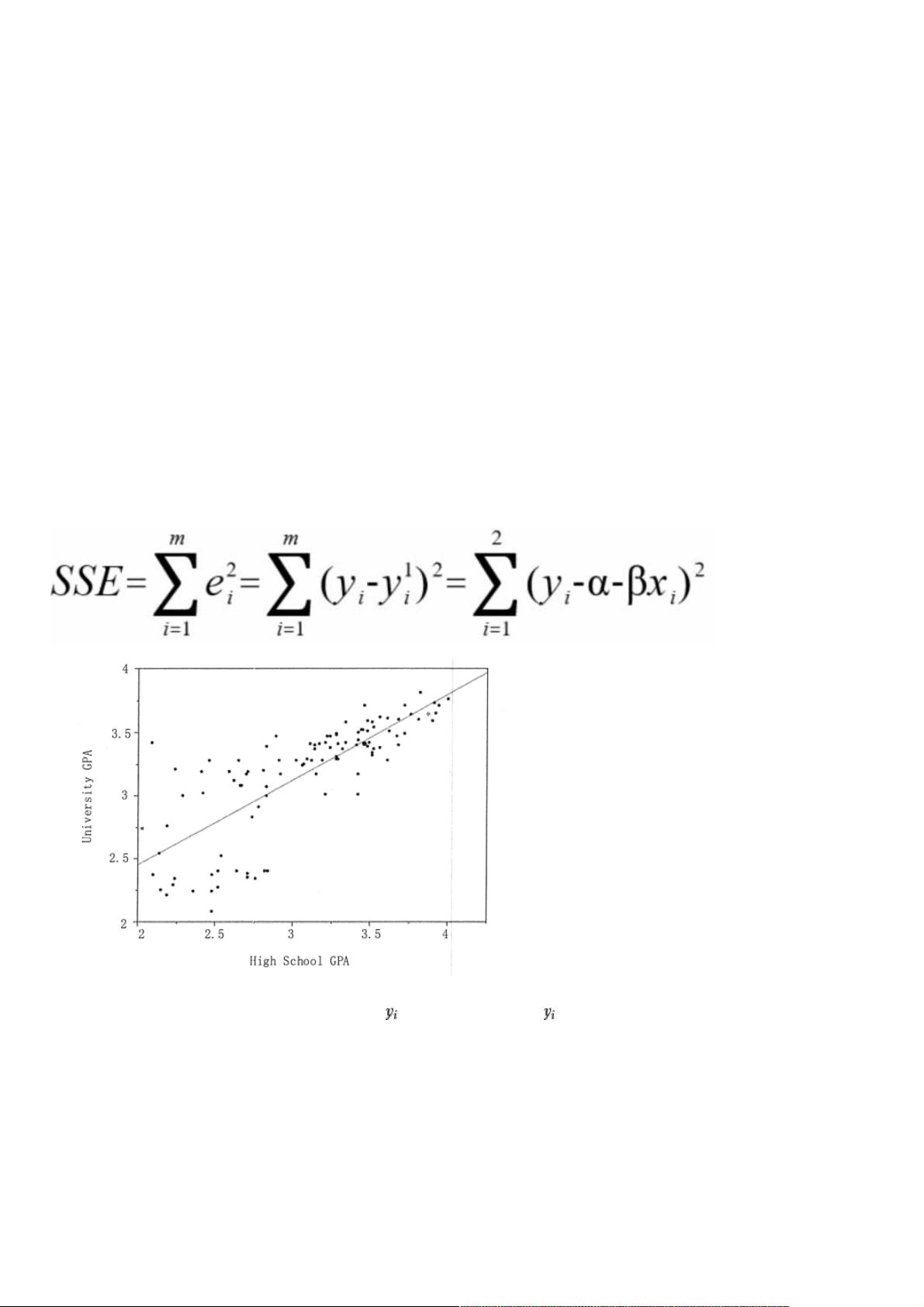
"回归分析是一种统计学方法，用于根据一组变量预测另一个变量。它通过寻找最佳模型来连接输入变量和输出变量，分为一元回归和多元回归，以及线性回归和非线性回归。线性回归是其中最常见的，包括一元和多元形式，用于建立连续因变量与一个或多个自变量之间的线性关系。" 回归分析预测技术是统计学中重要的预测和建模工具，主要用于探索变量间的关系并进行预测。这个技术的基础在于理解变量之间的关联性，以预测未知的或未来的值。回归分析可以根据自变量的数量、因变量的类型以及回归线的形状进行分类。 1. 自变量数量分类： - **一元回归**：仅有一个自变量与因变量相关联，用于构建简单的预测模型。 - **多元回归**：包含两个或更多自变量，能够考虑多个因素对因变量的影响，提高预测的准确性。 2. 因变量类型分类： - **线性回归**：因变量是连续的数值型数据，模型假设因变量与自变量之间存在线性关系。一元线性回归简单直观，通过最小二乘法找到最佳拟合线，使得数据点到这条直线的垂直距离（误差）平方和最小。公式为 Y = a + bx + e，其中a是截距，b是斜率，e是误差项。 - **非线性回归**：因变量与自变量的关系不是线性的，需要使用更复杂的函数来拟合数据，如二次、指数或对数函数。 3. 回归线形状分类： - **一元线性回归**：一个自变量与一个因变量之间通过一条直线进行建模，适用于简单直观的关系描述。 - **多元非线性回归**：涉及多个自变量，且它们与因变量之间的关系是非线性的，可能需要采用曲线或更复杂函数来拟合。 线性回归尤其在数据分析中广泛应用，因为它易于理解和解释。然而，对于非线性关系的数据，需要选择适当的非线性模型，如多项式回归、指数回归或对数回归等。回归模型的评估通常依赖于残差分析、R^2值、调整R^2值以及模型的拟合优度。 回归分析不仅用于预测，还可以用来测试假设、探索变量间的因果关系以及控制其他变量的影响。在实际应用中，特征选择、模型简化、过拟合和欠拟合等问题也需考虑。回归分析是理解和预测复杂现象的强大工具，它能帮助我们从大量数据中提取有价值的信息，为决策提供科学依据。