162 IEEE TRANSACTIONS ON SEMICONDUCTOR MANUFACTURING, VOL. 28, NO. 2, MAY 2015
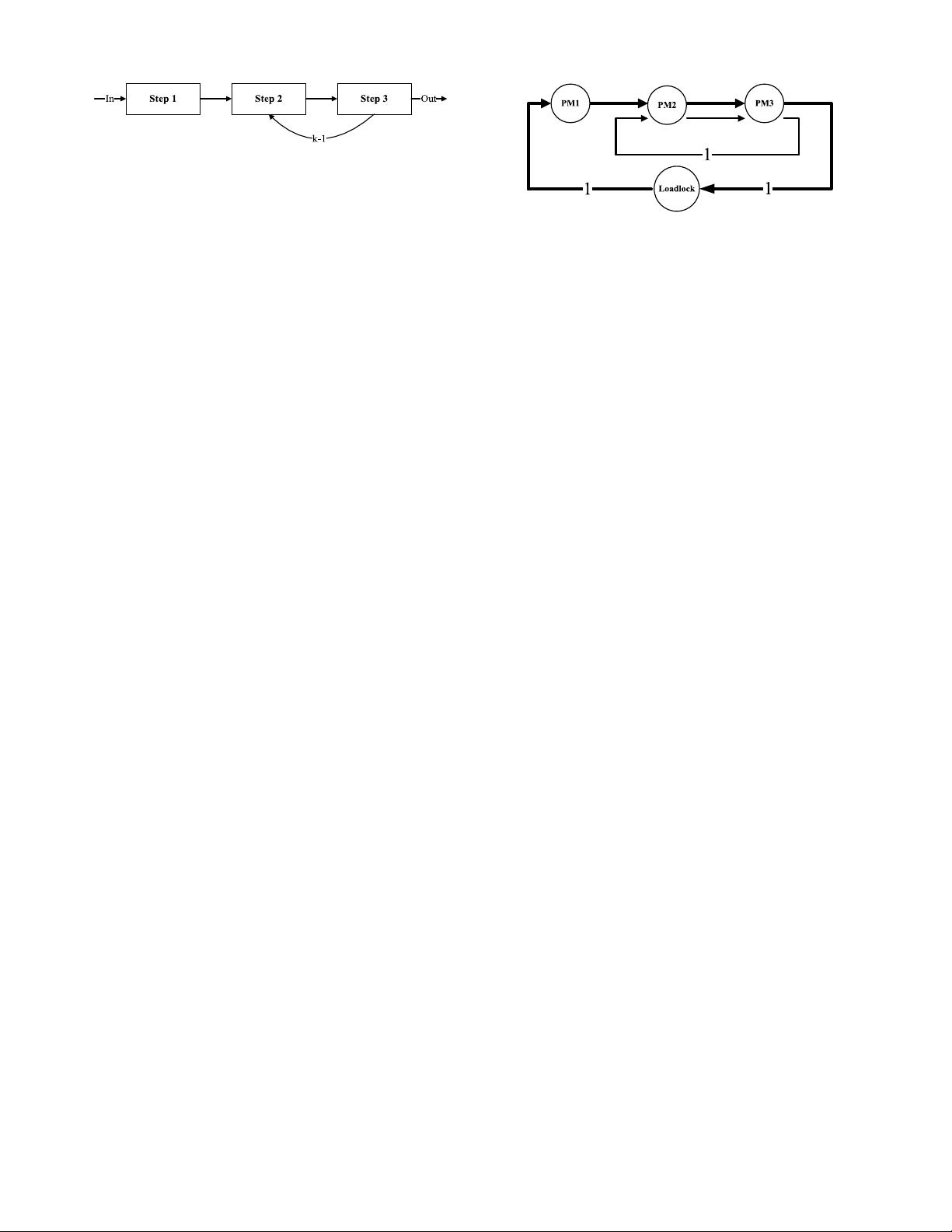
Fig. 2. Wafer flow for ALD process.
is typical and thus considered as an example in this paper.
For an ALD process, the thickness of the deposition layer is
determined by the number of revisiting times [15]. In an ALD
process, there are three steps, and a wafer visits Step 1 once,
and then Steps 2 and 3 for k ≥ 2 times as shown in Fig. 2,
where k is determined by a process plan. Let d
i
be the number
of PMs for Step i, then the wafer flow pattern for ALD can
be denoted as (d
1
,(d
2
, d
3
)
k
) with (d
2
, d
3
)
k
being the revis-
iting process. Often, when a wafer revisits a step it requires
exactly the same processing environment as it previously vis-
its this step. Consequently, each step is composed of only
one PM, or d
1
= d
2
= d
3
= 1. Then, it is assumed that
PM
1
,PM
2
, and PM
3
are used to process wafers at Steps 1–3,
respectively. Thus, the wafer flow pattern of an ALD process
can be denoted as (PM
1
,(PM
2
, PM
3
)
k
) with (PM
2
, PM
3
)
k
being a k-revisiting process. Without loss of generality and
to make the paper easy to follow, we assume that k = 2,
i.e., (PM
1
,(PM
2
, PM
3
)
2
).
B. Activity Description
There are several processing steps in a cluster tool for wafer
fabrication. The LLs can also be seen as a wafer processing
step. Hence, we treat the LLs as Step 0. According to [29], in
operating a cluster tool, PM activities follow the robot tasks.
Thus, it is critically important to schedule robot activities.
They include unloading a wafer from a PM, moving from
a PM to another with a wafer carried, loading a wafer into
a PM, moving from a PM to another without carrying a wafer,
and waiting. The key is to schedule the robot activities given
the tool’s status and process requirements. We use u
i
and l
i
to denote the robot unloading and loading a wafer from and
into PM
i
, i ∈ N
3
= {1, 2, 3}, respectively. As mentioned in
Section I, a swap strategy is efficient for scheduling dual-arm
cluster tools. A swap operation at PM
i
is executed as follows:
the robot holds a wafer in one arm → unloads a processed
wafer from PM
i
by the other arm → the robot rotates → loads
arawwaferintoPM
i
. In this way, a swap operation at PM
i
is
completed. It follows from this process that l
i
and u
i
together
with a rotation form a swap operation at Step i, i ∈ N
3
, and
we use s
i
to denote it. We use m
ij
to denote the robot mov-
ing from Steps i to j. In this paper, Steps 2 and 3 together
form a revisiting process. Therefore, m
32
represents the robot
moving from Steps 3 to 2.
For the purpose of scheduling, the temporal aspect for each
activity is necessary. The time taken for unloading a wafer is
denoted as α. Similarly, the time taken for loading a wafer
into a PM and moving from a PM to another are denoted as
β and μ, respectively. Although a swap operation includes
unloading and loading, the time taken for a swap operation is
not simply their sum. We use λ to denote its time. Besides
the robot activities, we use a
i
to denote the wafer processing
time at Step i, i ∈ N
3
.
Fig. 3. Wafer flow process by using one-wafer schedule.
C. One Wafer Scheduling Strategy
Let us recall how to obtain an optimal periodic schedule
for the k = 2 case. We use m
ij
to denote robot moving from
PM
i
to PM
j
.Letl
0
and u
0
denote robot’s loading and unload-
ing a wafer into and from an LL, respectively. In the revisiting
process (PM
2
, PM
3
)
2
, robot’s task sequence σ
1
=swapping
at PM
3
→ m
32
→ swapping at PM
2
→ m
23
forms a cycle
and it is called a local cycle. Sequence σ
2
=swapping at
PM
3
→ m
30
→ l
0
→ u
0
→ m
01
→ swapping at PM
1
→
m
12
→ swapping at PM
2
→ m
23
forms a cycle involving
all PMs once and it is a global cycle. A one-wafer schedule
should contain one local and one global cycle as shown in
Fig. 3. It is optimal in terms of cycle time according to [23].
Let M = {S
1
, S
2
, S
3
, S
4
} denote a state of the system,
where S
i
= {W
d
(q)}, i ∈ N
3
, and W
d
(q)isthed-th wafer
released to the system with its q-th operation being processed
in PM
i
(Step i). S
4
= {R
j
(W
d
(q)} represents the d-th wafer
held by the robot with its q-th operation to be processed at
Step j, j ∈ N
3
. For an optimal one-wafer steady-state sched-
ule, according to [23], the tool should start from state M
i
= {W
3
(1), W
1
(2), W
2
(3), R
1
(W
4
(1))} which is called the
first desired steady state. At this state, the 3rd, 1st and 2nd
wafers are being processed in PM
1
, PM
2
, and PM
3
for their
1st, 4th, and 3rd operations, respectively. At the same time, the
robot holds the 4th wafer with the 1st operation to be processed
at Step 1. From this state, by performing σ
3
=swapping
at PM
1
→ m
12
→ swapping at PM
2
→ m
23
, the system
enters state M
i+1
= {W
4
(1), W
3
(2), W
2
(3), R
3
(W
1
(5))}. Then,
by executing σ
1
, it reaches M
i+2
= {W
4
(1), W
2
(4), W
1
(5),
R
3
(W
3
(3))}. Finally, by executing σ
4
=swapping at PM
3
→
m
30
→ l
0
→ u
0
→ m
01
, M
i+3
= {W
4
(1), W
2
(4), W
3
(3),
R
1
(W
5
(1))} is reached. Notice that σ
3
and σ
4
together form
a global cycle, and M
i
and M
i+3
are equivalent. Therefore,
a period including a local and a global cycle is formed. During
this period, one wafer is unloaded from the LLs, while another
is completed and returns to the LLs.
Next, we analyze how the system can optimally enter the
first desired steady state from the idle state.
III. S
TART-UP TRANSIENT PROCESS SCHEDULING
In order to schedule the transient process from the idle state
to the required steady state, the program evaluation and review
technique (PERT) is applied based on network techniques.
By PERT, a network model is used to describe graphically the
precedence relationships of the activities in a project. Such
a network model is called a PERT model. The PERT has been
used in scheduling transient processes of a cluster tool [6].









