MIT电力电子课程：DC/AC逆变器与傅立叶变换解析

"这篇文档是麻省理工学院(MIT)的电力电子课程笔记，由D.Perreault教授主讲，重点讲述了DC/AC逆变器的相关知识，包括傅立叶变换在信号分析中的应用和逆变器的结构设计。" 在电力电子领域，傅立叶变换是一个关键工具，用于分析和理解周期性信号。它能够将复杂的周期性信号分解为无限多个简单正弦和余弦波的叠加。公式表示为： \[ \sum_{n=-\infty}^{\infty} c_n e^{jn\omega_0 t} \] 其中，\( c_n \)是傅立叶系数，\( \omega_0 \)是基频，\( n \)是谐波次数。对于实数信号，这些系数可以进一步分为\( a_n \)（对应于正弦项）和\( b_n \)（对应于余弦项）。 对于特定类型的函数，傅立叶系数具有特定性质： 1. 偶函数\( x(t)=x(-t) \)的傅立叶级数中不含\( b_n \)，因为\( \sin \)函数是奇函数，其乘积的积分等于零。 2. 奇函数\( x(t)=-x(-t) \)的傅立叶级数中不含\( a_n \)，因为\( \cos \)函数是偶函数，其乘积的积分也等于零。 3. 关于原点对称的函数\( x(t)=x(t-T/2) \)没有偶数次谐波分量\( a_{2n}=0 \)和\( b_{2n}=0 \)，因为积分的前半部分和后半部分会相互抵消。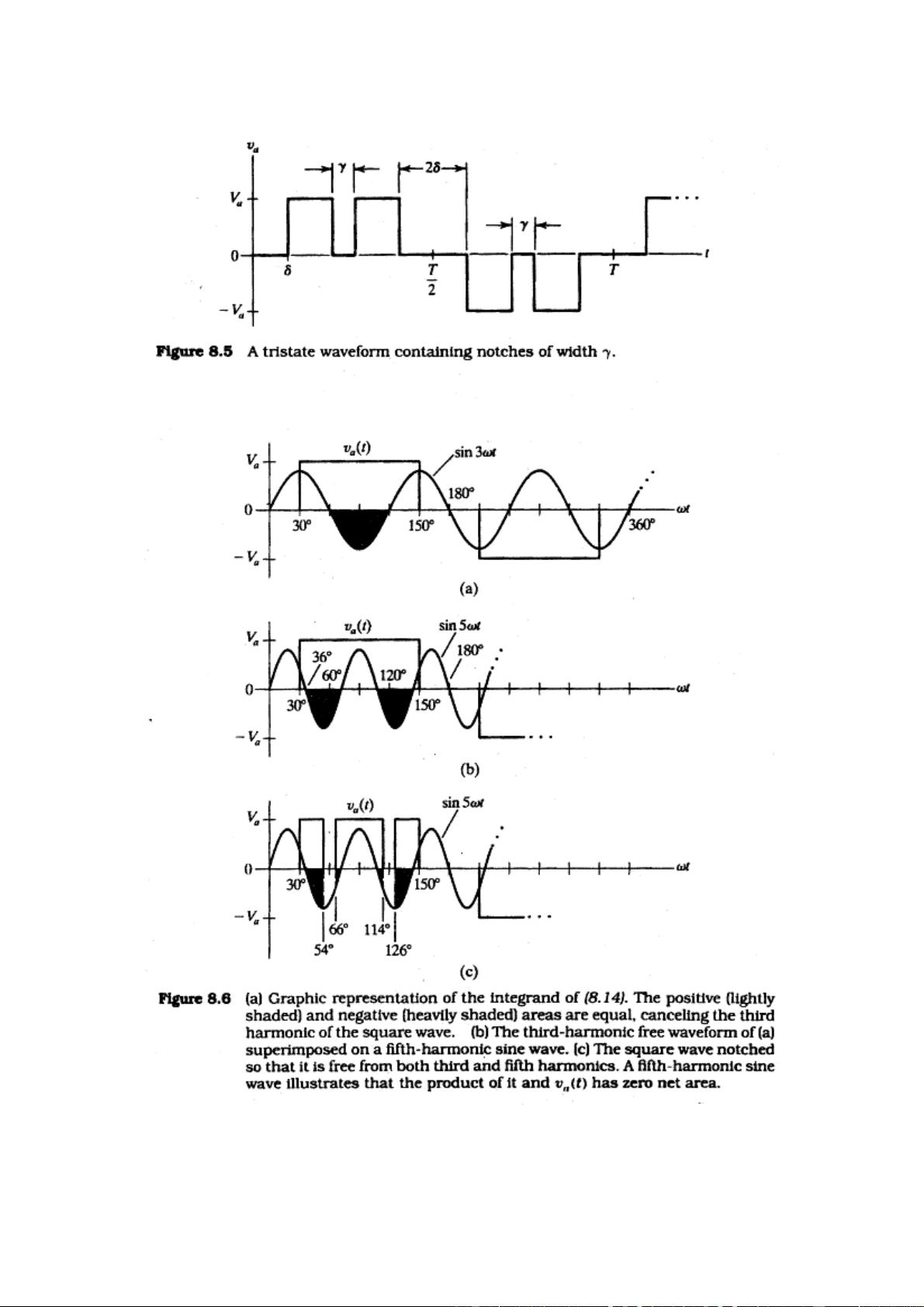 逆变器的目标是将直流电源转换为交流输出。这种转换通常通过开关电路来实现，如MOSFET和反并联二极管的组合。为了生成正弦波形，一种常见方法是采用脉宽调制(PWM)技术。在最简单的PWM策略中，每个开关在一个周期内只导通一次，这会产生含有奇数次谐波的半波对称波形。 当PWM占空比\( δ \)为0时，输出电压包含的是基波以及奇数次谐波，例如3次、5次和7次谐波。通过调整\( δ \)，可以控制基波和谐波的幅度。为了得到更纯净的正弦波输出，通常需要通过输出滤波器去除谐波。然而，由于低次谐波的频率接近基波，滤除它们较为困难。 总结来说，MIT电力电子课程笔记主要探讨了傅立叶变换在信号分析中的应用，以及如何利用PWM技术设计逆变器，以直流电源生成接近正弦波的交流输出，并讨论了如何通过调整PWM占空比来控制输出波形的品质。这个过程涉及到谐波的产生、控制以及滤波，这些都是电力电子系统设计中的核心概念。