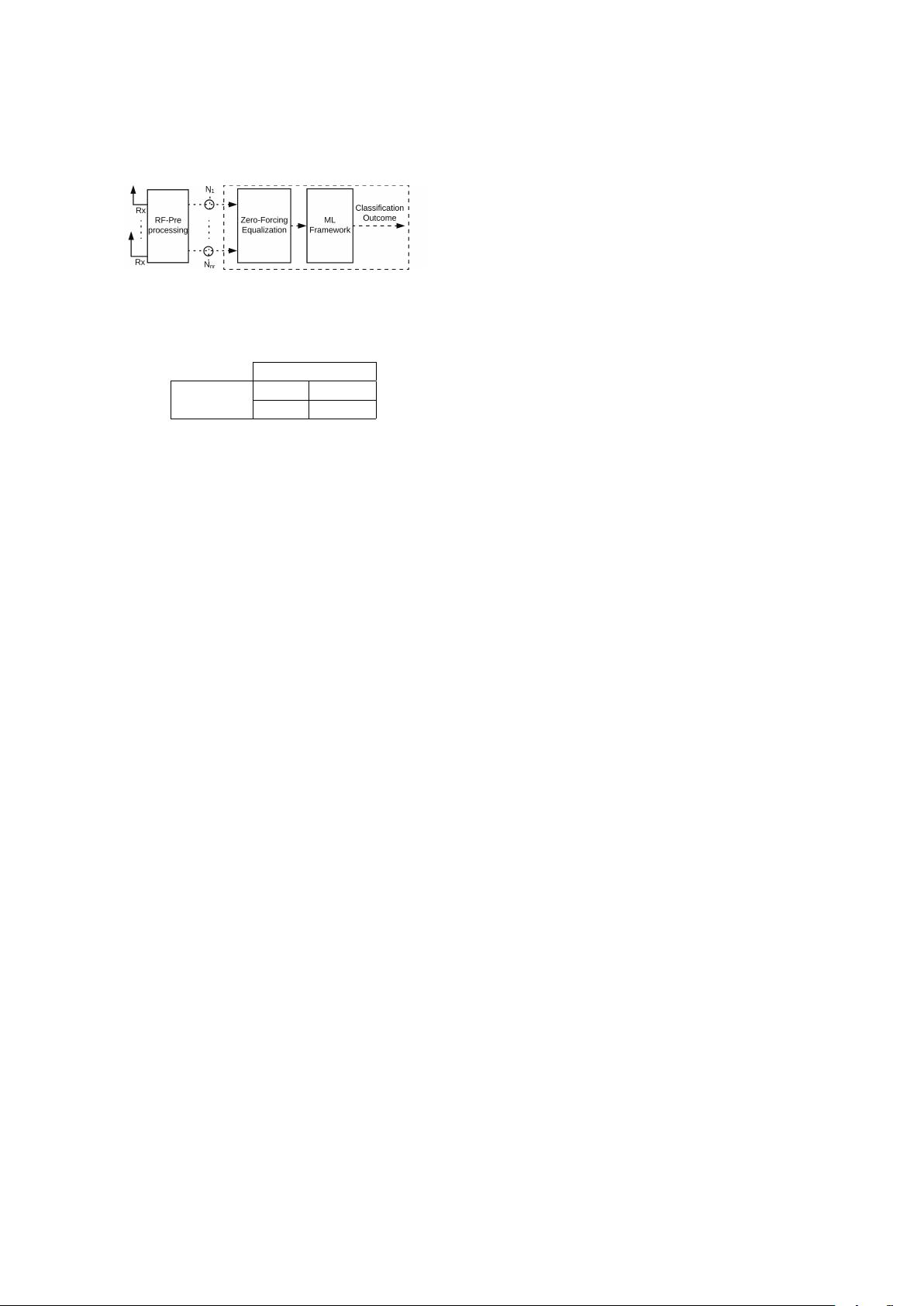
Shah and Dang / Front Inform Technol Electron Eng in press 3
Fig. 1 Overall process flow diagram of the proposed
study
Table 1 Alamouti STBC Coding
Time Slots
Antennas
s
2k+1
−s
∗
2k+2
s
2k+2
s
∗
2k+1
paper we propose to use the symbols after ZF equal-
ization for ML based classification.
For a MIMO system with N
t
transmit and N
r
receive antennas, the received signal vector is given
by :
R = HS + N (1)
In equation (1), R is the receive data vector of
dimension (N
r
× 1), H is the block-fading Rayleigh
distributed channel matrix of size (N
r
× N
t
) and N
is the additive white Gaussian noise (AWGN) vector
of size (N
r
× 1) with variance (σ
2
n
).
The signal mo del for Alamouti-STBC (2 × 2, , 2 × 1)
and for STTD (4 × 4) transmit and receive antenna
configuration is further explained in the following
subsections.
2.1 Alamouti-STBC for 2 × 2 MIMO configu-
ration
Alamouti block coding is a transmit diversity
technique which can be used in a 2 × 1 multiple-
input and single-output (MISO) or 2 × 2 MIMO
configuration (Alamouti, 1998). We consider the
2 × 2 MIMO configuration to elaborate the sig-
nal model and achieve a generalized received sig-
nal vector form. Table 1 represents the Alamouti-
STBC scheme, where (s
2k+1
) and (s
2k+2
) are sym-
bols transmitted by antenna 1 and 2 respectively at
time slot (2k + 1). Similarly,(−s
∗
2k+2
) and (s
∗
2k+1
)
are symbols transmitted by antenna 1 and 2 respec-
tively at time slot (2k + 2). Here, [*] represents
the conjugate and k ∈ 0, 1, ....L/2, where L is the
block length of data symbols. The process of re-
ceived vector combination for multiple antennas at
different time-slots is elaborated for the Alamouti-
STBC (2 × 2) configuration, which is subsequently
generalized for other scenarios.
The received signal at antenna (N
r
= 1) and
(N
r
= 2) at time slot (2k+1) is given by :
(2k+1)
r
1
= h
11
s
2k+1
+ h
12
s
2k+2
+
(2k+1)
n
1
(2)
(2k+1)
r
2
= h
21
s
2k+1
+ h
22
s
2k+2
+
(2k+1)
n
2
(3)
In equations (2) and (3), overset is used to de-
note the time slot and the subscript emphasizes the
antenna number. The received signal at both anten-
nas at time slot 2k+2 can be given by:
(2k+2)
r
1
= h
11
(−s
∗
2k+2
) + h
12
s
∗
2k+1
+
(2k+2)
n
1
(4)
(2k+2)
r
2
= h
21
(−s
∗
2k+2
) + h
22
s
∗
2k+1
+
(2k+2)
n
2
(5)
By taking the conjugate of equations (4 , 5) and
rearranging to get a combined received vector for
both antennas at time slots (2k + 1) and (2k + 2) we
get:
(2k+1)
R =
(2k+1)
r
1
(2k+1)
r
2
=
[
h
11
h
12
h
21
h
22
][
s
2k+1
s
2k+2
]
+
(2k+1)
n
1
(2k+1)
n
2
(6)
(2k+2)
R =
(2k+2)
r
∗
1
(2k+2)
r
∗
2
=
[
h
∗
12
−h
∗
11
h
∗
22
−h
∗
21
][
s
2k+1
s
2k+2
]
+
(2k+2)
n
∗
1
(2k+2)
n
∗
2
(7)
Equations (6 and 7) represent the combined re-
ceived vectors for antennas 1 and 2 at time slots
(2k + 1) and (2k + 2) respectively. By combining the
received vectors for different time slots in equations
(6 and 7) we get:
←→
R =
←→
H S +
←→
N (8)
Here,| ↔ | represents the concatenation operation
where
←→
R =
(2k+1)
R
(2k+2)
R
,
←→
H =
(2k+1)
H
(2k+2)
H
and
←→
N =
(2k+1)
N
(2k+2)
N
.









