混合场理论：p-adic与实数的标量场交互

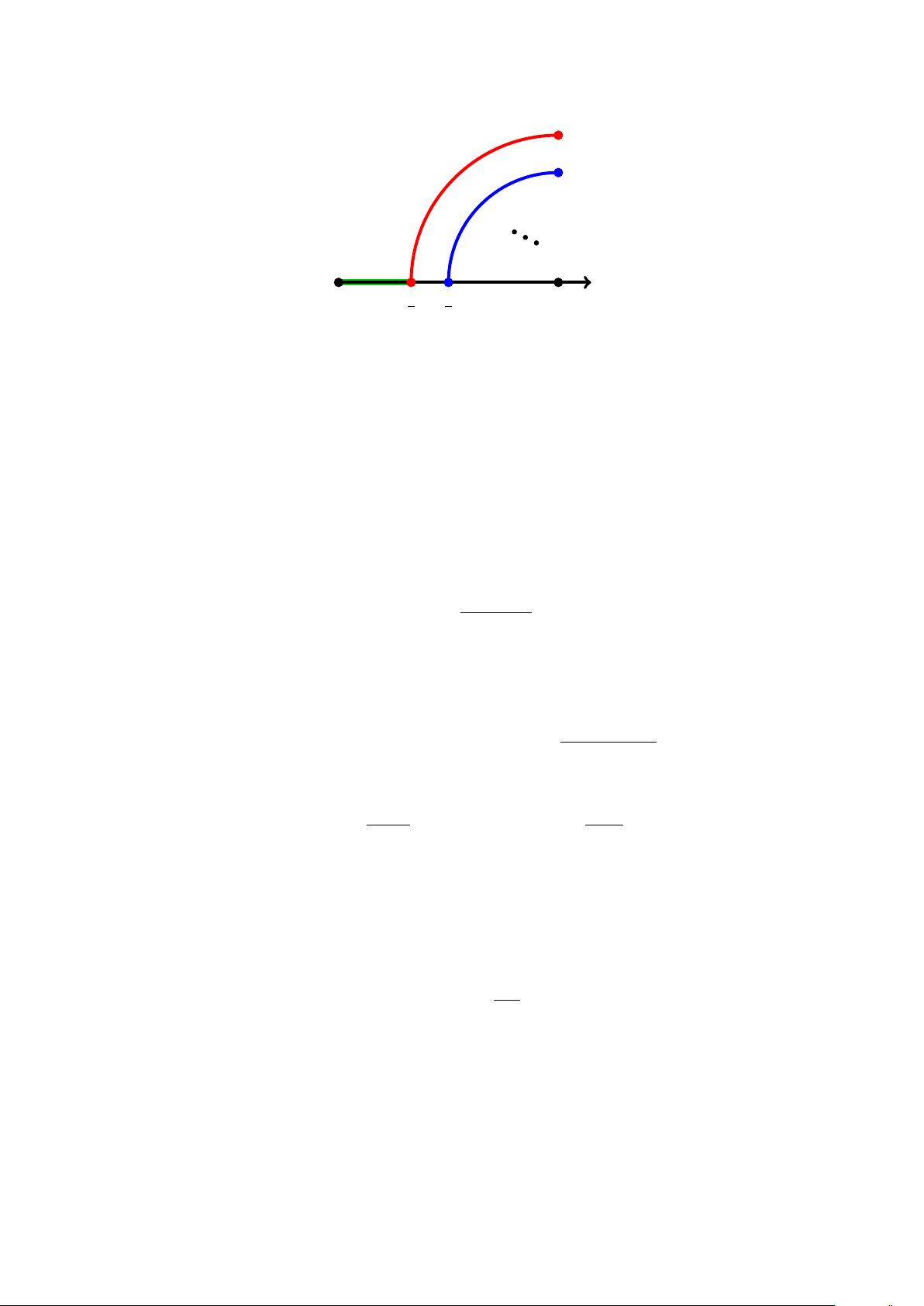
"混合场理论是研究实数与p-adic数直接乘积上的标量场理论，其中引入了可调整的动态缩放指数z，使得高斯理论呈现出固定点线。在z等于1/3时，Wilson-Fisher不动点的一个分支与高斯理论的固定点线相接。在扰动可访问的区域内，该理论计算了Wilson-Fisher不动点的标准临界指数，并包含了动态临界指数的循环校正。研究发现，经典传播器在实数方向上存在振荡行为，但振幅可通过非微调理论参数的方式指数级减小。在傅立叶空间中，二次循环校正也揭示了类似振荡，同样可以通过调整参数来显著抑制。此外，对于紧凑的p-adic额外维，非线性的标量场理论允许一种一致截断的形式，仅保留有限的Kaluza-Klein模用于非紧凑方向上的有效理论。" 在本文中，作者 Steven S. Gubser, Christian Jepsen, Ziming Ji 和 Brian Trundy 深入探讨了混合场理论，这是一个涉及实数和p-adic数领域相互作用的理论框架。他们首先指出，通过在微观拉格朗日量中引入动态缩放指数z，可以实现高斯理论的固定点线。当z取值为1/3时，Wilson-Fisher不动点的一个分支与高斯固定点线相遇，这在统计物理和量子场论中具有重要意义，因为它表示了场的相变点。 进一步的分析集中在Wilson-Fisher不动点的临界指数上，这些指数在理论的可扰动区域内被计算出来，包括动态临界指数的循环校正。这提供了理解系统在接近相变时的行为的关键信息。有趣的是，研究发现即使在经典水平，传播器在实数方向上也表现出振荡性质，但这些振荡的强度可以被控制，无需精确调整理论参数就能使其显著减弱。 在傅立叶变换的空间中，作者还发现了由于二次循环校正导致的类似振荡。这表明在频域内，理论的性质也受到这种振荡的影响，不过这些振荡同样可以通过参数调整得到抑制。这一发现可能对理解和模拟复杂系统的动力学行为有重要影响。 最后，作者探讨了紧凑的p-adic额外维度情况下的非线性标量场理论。他们提出了一种一致截断的方法，允许在非紧凑方向上构建有效理论时只保留有限的Kaluza-Klein模式。这种方法对于简化理论模型、减少自由度并可能揭示额外维度的物理效应具有实际价值。 这项工作展示了混合场理论在理解和探索跨实数和p-adic数域的物理现象中的潜力，以及在处理复杂系统、相变和额外维度问题时的创新方法。