数据结构B卷：搜索二叉树与相关概念

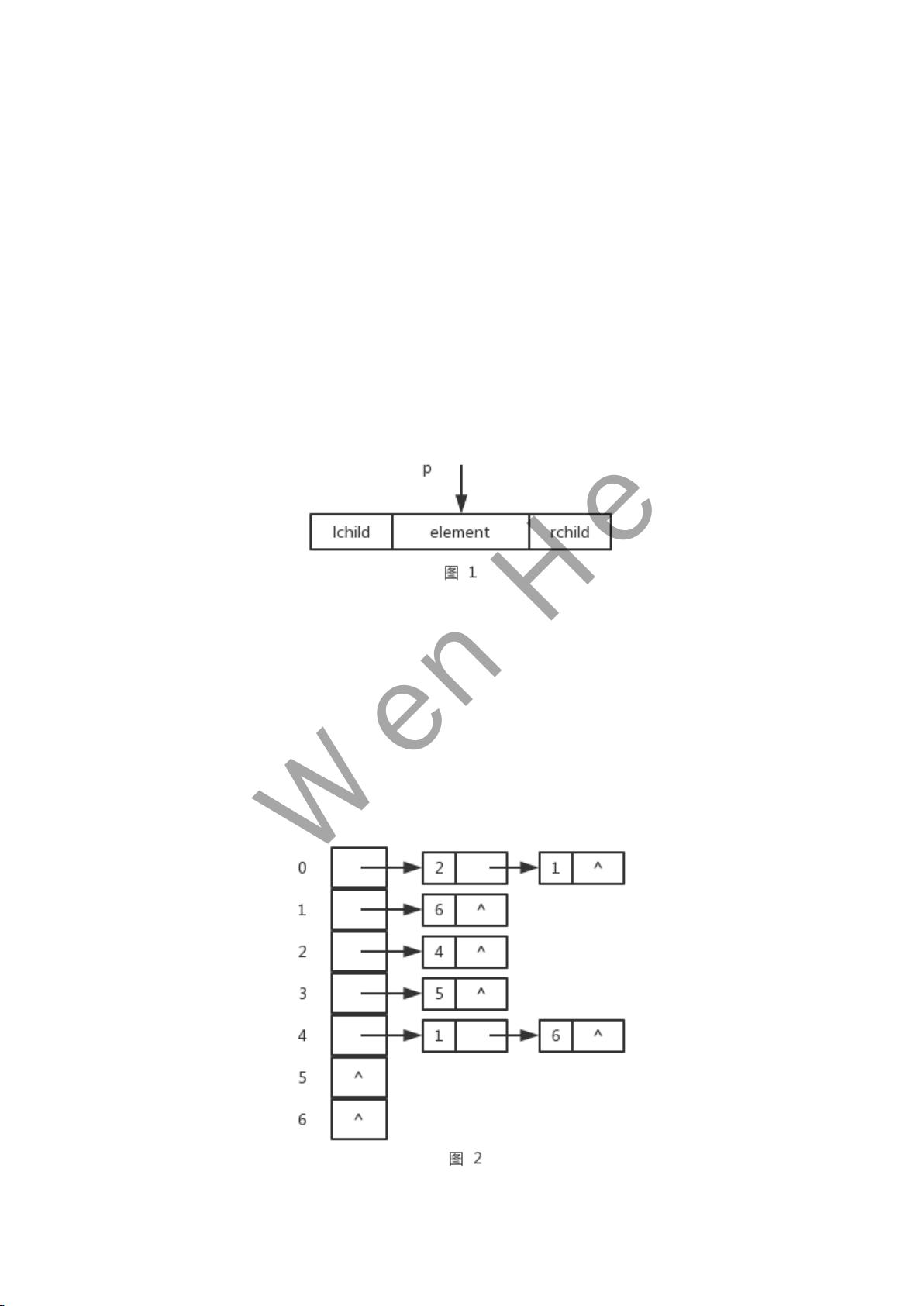
本题为南京邮电大学2016/2017学年第一学期《数据结构A》期末试卷（B卷）的部分题目，主要涉及数据结构的基础概念和算法分析。以下是部分题目详解： 1. 填空题： - 在给出的整数序列38, 43, 90, 29, 13, 78, 58中构建二叉搜索树，删除78后，由于78是比58大、比90小的节点，删除后可能影响到其父节点的平衡，具体根结点变化取决于删除操作后的调整。需要根据二叉搜索树的性质来确定新的根节点。 2. 结点链接表示： - 指针p指向叶结点的条件是它没有右子节点，即p->right == NULL。 3. 时间复杂度： - 两个嵌套循环的结构，外层循环执行n次，内层循环也执行n次，因此总的时间复杂度是O(n^2)。 4. 二叉树与森林的关系： - 对于一个有四棵树的森林，二叉树中根节点的左子树上结点个数等于前三棵树结点数之和，即n1 + n2 + n3。 5. 查找操作时间复杂度： - 当使用数组或链表等随机访问的数据结构存储线性表时，Find(i,x)的平均查找时间复杂度可以达到O(1)，因为可以直接通过索引定位元素。 6. 平均搜索长度： - 顺序搜索的平均搜索长度等于元素个数除以每个元素被找到的概率，由于所有元素搜索概率相等，所以平均搜索长度为n。 7. 图的入度： - 需要查看图G的邻接表，但题目中并未提供具体邻接表，无法直接计算顶点6的入度。入度通常指的是一个顶点连接的边的数量，如果是无向图，则入度等于出度。 8. 散列表冲突处理： - 散列函数h(key) = key % 11用于计算散列表的下标。当关键字21经过散列函数处理后，其下标将是21除以11的余数，即21 % 11。 9. 哈夫曼树： - 要求构建哈夫曼树且满足左孩子结点权值小于右孩子结点权值，这是一种典型的哈夫曼编码问题。计算加权路径长度（WPL）通常涉及到构建树的过程，最终结果需要通过递归或动态规划计算得出。 10. 冒泡排序时间复杂度： - 冒泡排序在最好情况下（输入已经排序）的时间复杂度为O(n)，因为只需一次遍历即可确认整个序列有序。 选择题： - 选项分析：A项错误，算法的优劣不仅与描述语言有关，也与计算机性能和数据结构等因素有关；B项正确，健壮的算法应对非法输入有正确的处理机制；C项错误，数据的逻辑结构独立于存储结构，存储结构改变可能影响实现方式，但逻辑结构不变；D项不全对。 这部分题目涵盖了数据结构的基本概念，如二叉搜索树、哈夫曼树、散列表、排序算法以及算法分析等知识点，解答时需要对这些理论有深入理解。