k
0
is the free-space wave number, and β is the propagation
constant. The equation can be also written as
[31]
−
∂
2
∂x
2
þ
∂
2
∂y
2
E þ
2k
2
1
Δ
a
2
ðx
2
þ y
2
ÞE ¼ðk
2
1
− β
2
ÞE; (4)
where k
1
¼ n
2
1
k
2
0
. The solutions can be found as
[32]
k
2
1
− β
2
¼ 2
2k
2
1
Δ
a
2
r
ðm
x
þ m
y
þ 1Þ; (5)
β ¼
k
2
1
− k
1
2
2Δ
p
a
ðm
x
þ m
y
þ 1Þ
s
≈ k
1
−
2Δ
p
a
ðm
x
þ m
y
þ 1Þ: (6)
From Eq. (
6) the effective index difference between two
neighboring modes is
Δn ¼
2Δ
p
ak
0
: (7)
The fundamental solution of the electrical field can be
approximated as the Gaussian function E
0
¼ Ae
−
x
2
þy
2
2σ
2
,
where σ is the standard deviation of the Gaussian function
as σ
2
¼
a
k
1
2Δ
p
[32,33]
. The integral of a Gaussian function
gives
ZZ
Ae
−
x
2
þy
2
2σ
2
dxdy ¼ 2πAσ
2
; ð8Þ
and the effective area of LP
01
is calculated as
A
eff
¼
RR
E
2
dxdy
2
RR
E
4
dxdy
¼ 2πσ
2
¼ 2π
a
k
1
2Δ
p
: (9)
The multiplication of the effective area and index differ-
ence thus leads to the relation below:
A
eff
Δn ¼ 2π
a
k
1
2Δ
p
2Δ
p
ak
0
¼
λ
2
0
2πn
1
: (10)
It is a constant at a fixed core index and wavelength.
When the constant is divided by the wavelength, the for-
mula is only related to the core index in the following form:
A
eff
Δn
λ
2
0
¼
1
2πn
1
: (11)
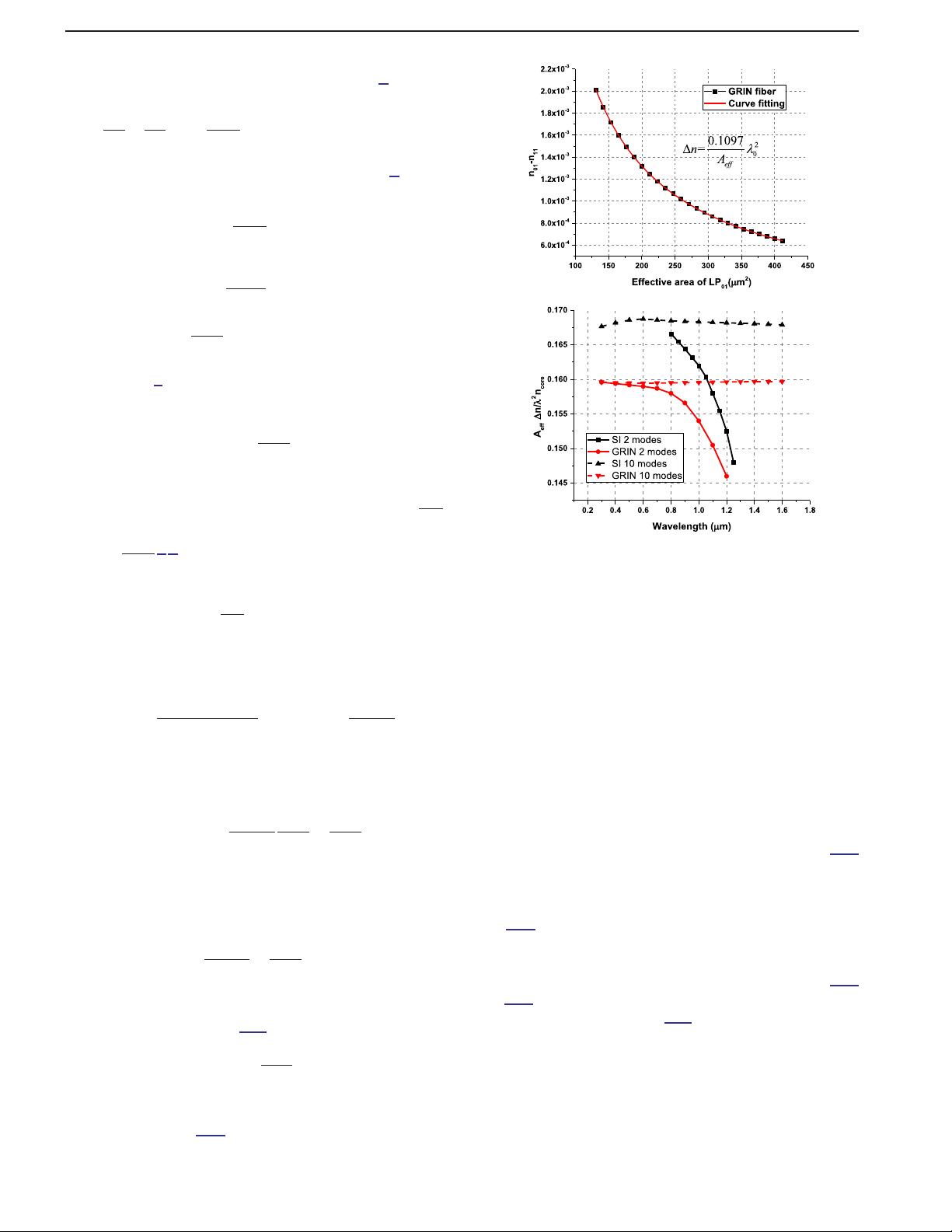
The value would be 0.1098 for a 1.45 core index. The fit-
ting curve is plotted in Fig.
2(a), showing a fitting coefficient
of 0.1097, which is almost the same as the analytical result.
To verify that the formula
ΔnA
eff
λ
2
0
is constant at different
wavelengths, the numerical simulation results as functions
of wavelength for SI or GRIN fibers with two or ten modes
are plotted in Fig.
2(b). The curves for two-mode fibers
show that the simulated value decreases slowly as the
wavelength increases because it is closer to the cutoff
condition at a longer wavelength. Far away from the cut-
off condition, the curves for SI or GRIN fibers with ten
modes demonstrate nearly constant values at different
wavelengths.
The previous simulation shows that the multiplica-
tion of the effective index difference and the effective
area of the fundamental mode is always a constant for
common SI and GRIN FMFs. To generalize the conclu-
sion, fibers with various index profiles shown in Fig.
3(a)
are simulated, including two-step fiber, GRIN fiber with
a trench, triangular-size profile, and index profile propor-
tional to the reversed LP
11
intensity profile. The curves in
Fig.
3(b) show that the constants for those index profiles
are always smaller than that of the SI fiber.
MCFs are also considered, with the first supermode pro-
files for three-core or six-core fibers shown in Figs.
4(a)
and
4(b). The curves of effective index difference vs. effec-
tive area are plotted in Fig.
4(c). Here the effective index
difference is from the first two supermodes, and the effec-
tive area is for the first supermode. The results also show
the existence of the limit of the constant no matter what
the index profile is.
For FMFs and MCFs with various index profiles, the
multiplication of effective index difference and effective
(a)
(b)
Fig. 2. (a) Effective index difference vs. effective area curve
fitting for graded-index fiber. (b) The multiplication constant
as a function of wavelength for SI or GRIN fibers with two or
ten modes.
COL 18(4), 040601(2020) CHINESE OPTICS LETTERS April 2020
040601-3


















