动态规划解析：多阶段决策与最短路径问题

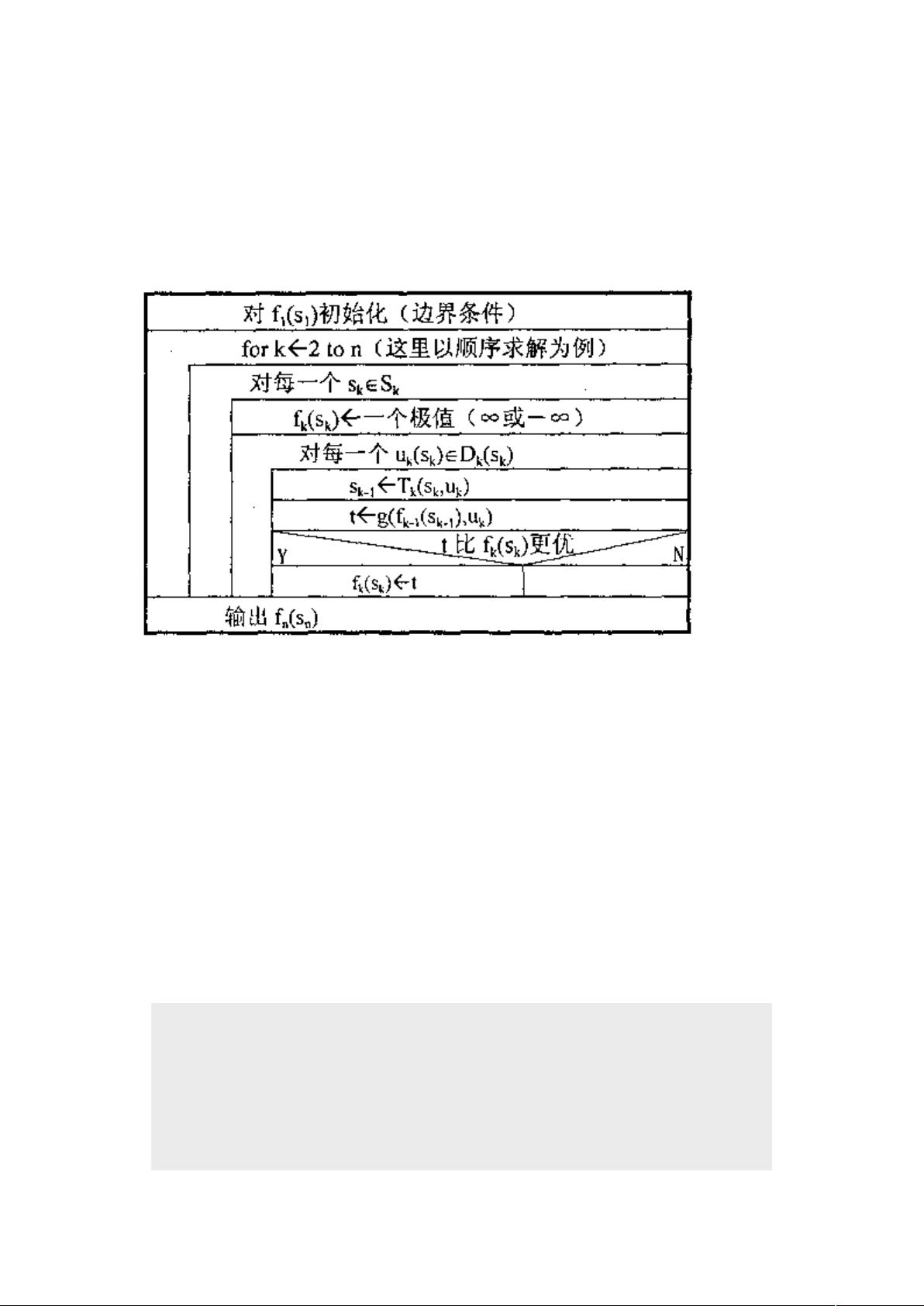
"该资源是一个关于动态规划的教程，通过讲解动态规划的概念和一个具体的最短路径问题，帮助学习者理解和应用动态规划方法解决实际问题。" 动态规划是一种解决最优化问题的有效算法，尤其适用于那些具有重叠子问题和最优子结构性质的问题。这种方法将复杂的问题分解成一系列更小的子问题，然后通过存储和重用之前计算的子问题的解，避免重复计算，以达到高效求解的目的。 多阶段决策过程是动态规划的基本模型，它模拟了现实生活中需要逐步决策的情况。在这个过程中，每个阶段都有多个可能的状态，并且每个决策都会影响后续阶段的结果。决策的选取基于当前状态，并且影响着最终的整体最优解。 例如，最短路径问题是动态规划的一个经典应用。在这个问题中，我们通常使用Dijkstra算法或Floyd-Warshall算法来寻找图中两点之间的最短路径。在给出的例子中，从城市A到城市E的最短路径可以被分阶段分析，每一步都计算从当前节点到目标节点的最短距离。通过逐步回溯，我们可以计算出从每个阶段的每个状态到终点E的最短距离，最终得到全局的最短路径。 在动态规划中，我们通常定义一个状态转移方程来描述从一个阶段到下一个阶段的决策过程。对于最短路径问题，这个状态转移方程可以表示为Fk(xk) = min{d(xk, xk+1) + Fk+1(xk+1)}，其中Fk(xk)是从状态xk到终点的最短距离，d(xk, xk+1)是从状态xk到状态xk+1的距离。 在上述例题中，我们按照阶段反向计算，从最后阶段（K=4）开始，逐步向前推进，直到第一阶段（K=1）。每个阶段我们都会更新所有可能的初始状态到终点的最短距离，最终得到起点A到终点E的最短路径。 总结来说，动态规划是通过分阶段分析问题，构建状态空间，并利用最优子结构来找到全局最优解的方法。通过学习和掌握动态规划，我们可以解决诸如最短路径、背包问题、最长公共子序列等一系列复杂问题。在实际应用中，动态规划不仅可以应用于计算机科学，还广泛应用于经济学、工程学等领域。