University of Kentucky Mech. Eng. - Acoustic BEM Lecture

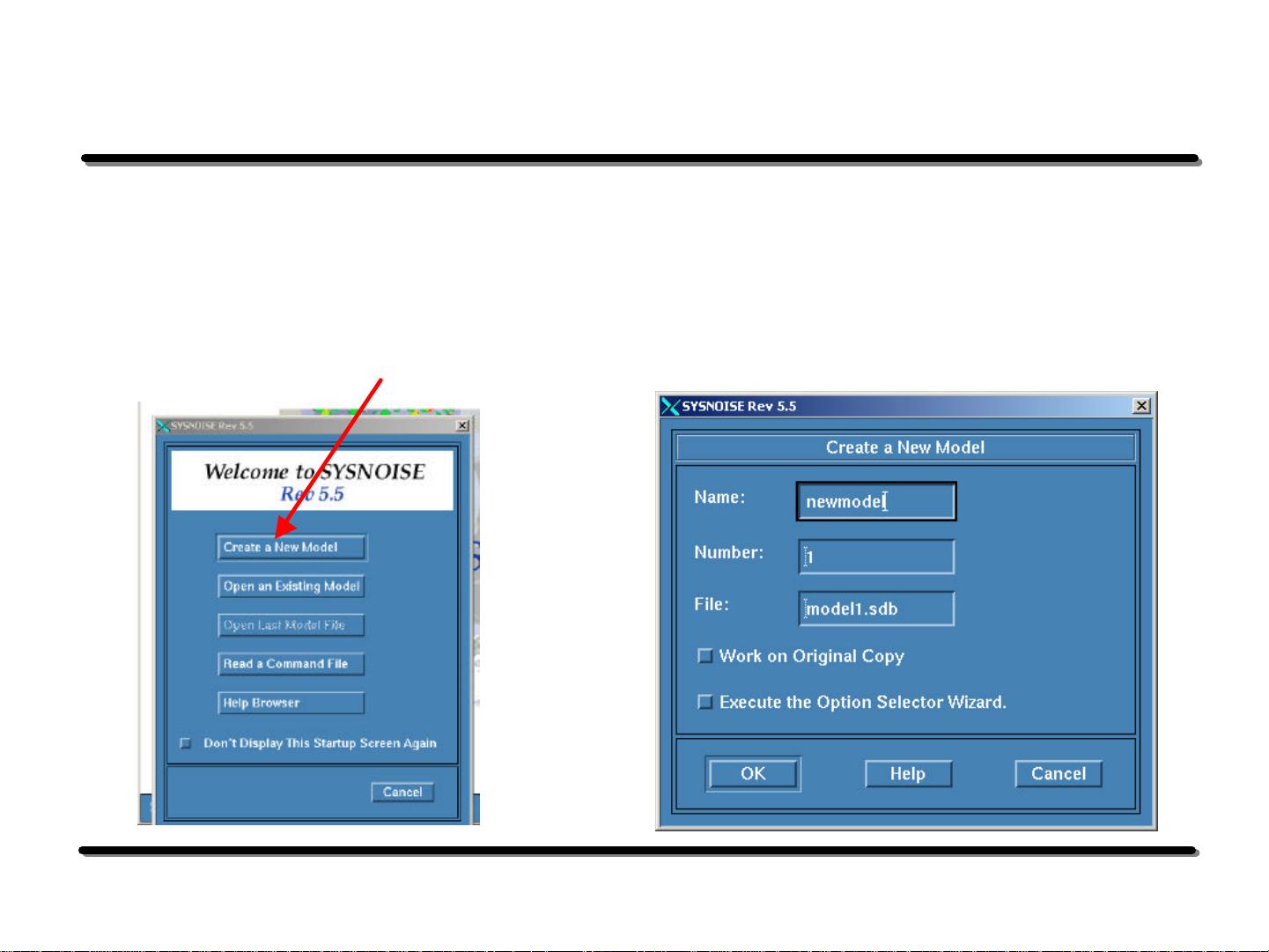
"sysnoise turtrial chapter 9 - 针对机械工程的振动声学设计的讲座，采用PPT格式，重点介绍了边界元方法在声学中的应用" 本资源是一份关于声学建模的学术讲座材料，来源于University of Kentucky的机械工程部门，主要探讨了边界元方法（BEM）在振动声学设计（Vibro-Acoustic Design）课程中的应用。以下是详细的知识点解析： 1. **边界元方法（Acoustic BEM）** 边界元方法是数值分析中的一种技术，特别适用于处理与边界条件密切相关的物理问题。在声学领域，它被用来求解声场的分布，尤其是在解决复杂的几何形状和非均匀介质中的问题时，具有一定的优势。 2. **概念描述** BEM的基本思想是只对问题的边界进行离散化，而不是整个区域。这使得在处理大型复杂结构时，计算量显著减少。 3. **预处理（Preprocessing）** - **网格（Mesh）**：在BEM中，需要将边界划分为一系列小的边界元素，这个过程称为网格划分。 - **边界条件**：定义边界上的声学特性，如声压、速度或辐射阻抗等。 4. **求解（Solution）** 这一步通常涉及解线性方程组，以找到边界上各点的未知声学变量。 5. **后处理（Post-Processing）** 在获得解决方案后，通过可视化和其他分析工具来解释和展示结果，如声压分布、声功率等。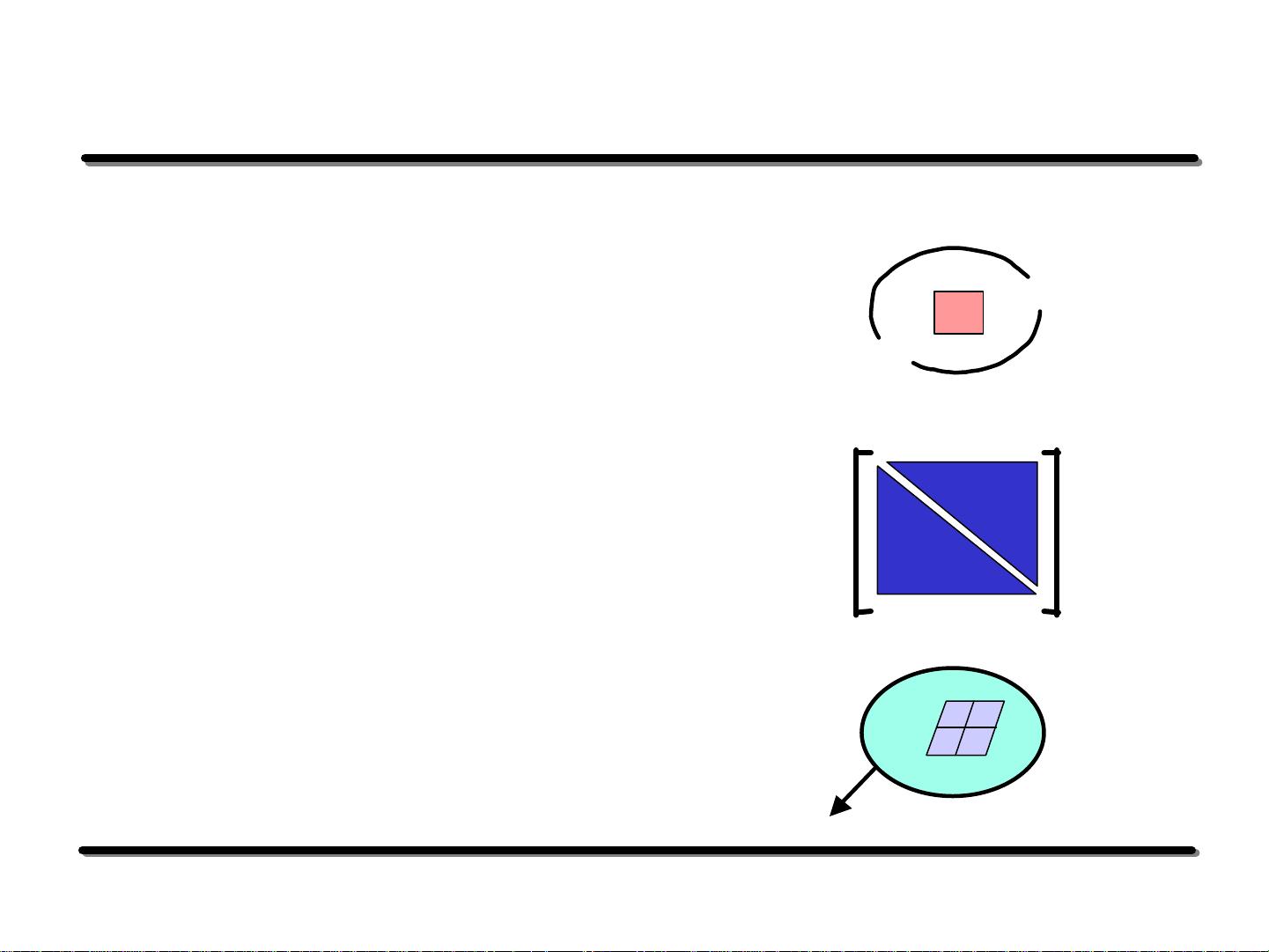 6. **FEM与BEM的比较** - **有限元方法（FEM）**：适用于对三维体积进行离散化，适合解决内部噪声分析，但计算模式较为昂贵，尤其是对于声辐射问题，除非使用接口有限元（I-FEM）。 - **边界元方法**：主要处理二维表面元素，易于计算声辐射，同时也擅长解决内部问题。 7. **数值方法概览** 讲座还涵盖了数值方法在不同分析类型中的应用，如室内噪声分析和辐射分析，其中声学边界元素特别用于这些目的。 8. **应用范围** 无论是室内噪声分析还是辐射分析，BEM都显示了其作为有效工具的潜力，特别是在只需要考虑边界条件的情况下。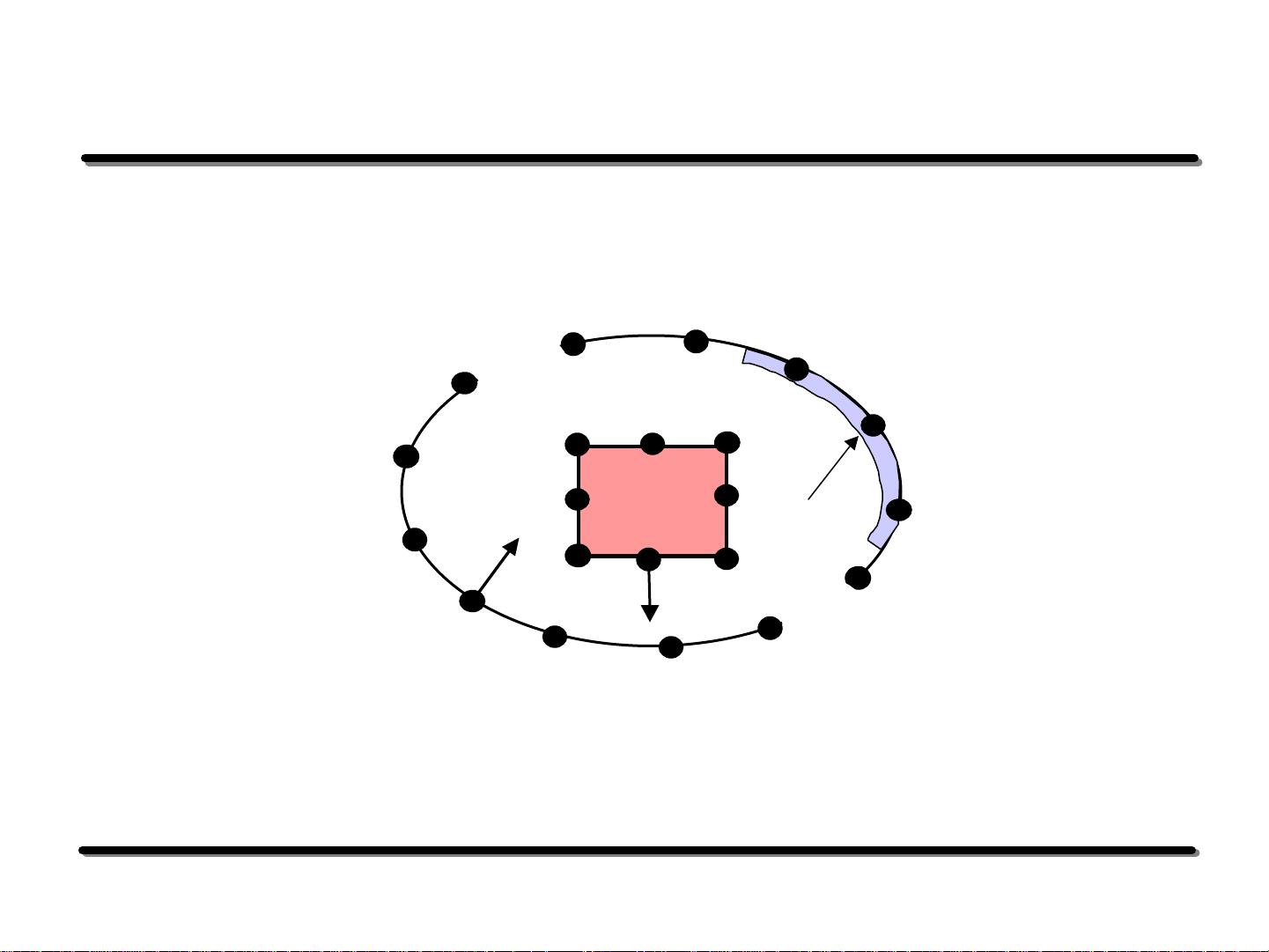 9. **2-D表面元素** 在声学BEM中，边界被划分为2-D表面元素，这是因为声波在传播过程中主要沿着边界进行交互。 这份资料详细阐述了如何利用边界元方法来理解和解决声学问题，特别是对于机械工程中的振动声学设计有着重要的理论和实践价值。