MATLAB曲线拟合实战:线性与多项式方法
需积分: 50 35 浏览量
更新于2024-10-23
收藏 277KB DOC 举报
"MATLAB插值与拟合"
MATLAB 是一个强大的数学软件,广泛应用于科学计算、数据分析和工程应用等领域。在处理实验数据时,插值与拟合是非常重要的技术,能够帮助我们理解和预测数据趋势。本文将详细介绍MATLAB中的线性拟合函数 `regress()` 和多项式曲线拟合函数 `polyfit()`。
1. **线性拟合函数:regress()**
`regress()` 函数用于执行一元线性回归分析,即通过最小二乘法寻找最佳的线性关系来拟合数据。它可以根据观测值 `y` 和自变量矩阵 `X` 计算出线性模型的参数。线性模型通常表示为 `y = Xβ + ε`,其中 `β` 是参数向量,`ε` 是随机干扰项,服从标准正态分布。`regress()` 返回的结果 `b` 即为 `β` 的估计值,`bint` 提供了这些参数的置信区间。此外,`r` 和 `rint` 分别是形状残差和残差的置信区间,`stats` 包含了 R² 统计量、F 值和 p 值等统计信息。通过实例,我们可以看到如何使用 `regress()` 来确定线性拟合方程的系数。
2. **多项式曲线拟合函数:polyfit()**
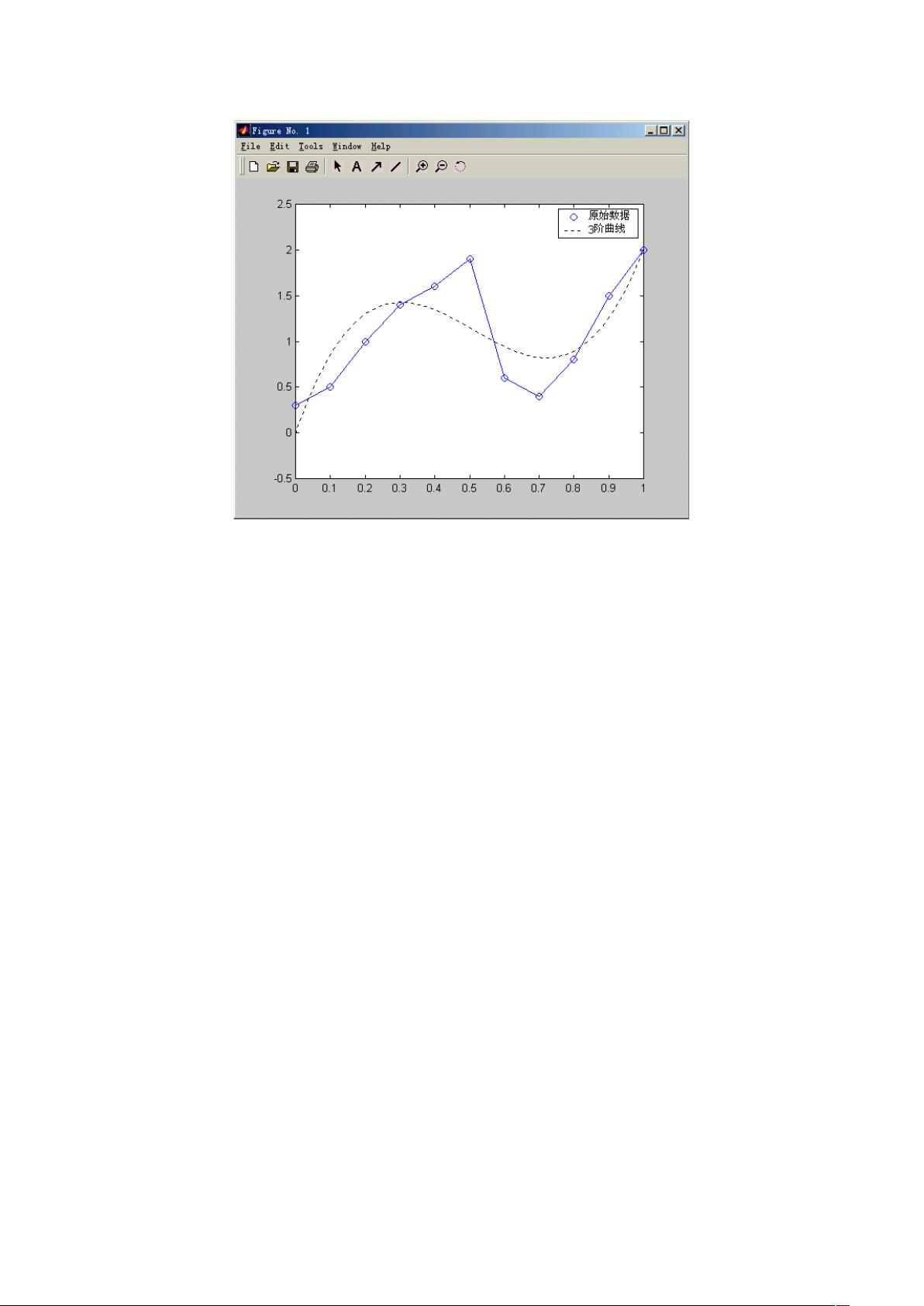
当线性拟合无法满足需求时,可以使用 `polyfit()` 进行多项式拟合。该函数允许我们找到一个特定阶数 `n` 的多项式,使数据点 `(x, y)` 最好地拟合。函数返回的向量 `p` 由多项式的系数组成,从最高次项到最低次项。`polyfit()` 结合 `polyval()` 可以用于预测新的数据点。例如,如果给定一组离散数据点,我们可以使用 `polyfit()` 来确定一个合适的多项式函数,从而描绘出数据的变化趋势。
在实际应用中,选择合适的拟合方法至关重要。线性拟合适用于数据呈线性关系的情况,而多项式拟合则适用于更复杂的数据结构。在选择拟合方法时,应考虑数据的特征、拟合的目的以及模型的复杂性。通常,我们需要评估拟合的质量,例如通过检查残差、计算 R² 值或使用统计检验(如 F 检验)来判断模型的显著性。
MATLAB 提供了丰富的工具,如 `regress()` 和 `polyfit()`,使得数据的插值与拟合变得简单易行。通过灵活运用这些函数,我们可以对数据进行有效的分析,揭示隐藏的模式,并对未来数据进行预测。在科学研究和工程实践中,正确地理解并运用这些方法对于得出准确结论至关重要。
点击了解资源详情
点击了解资源详情
204 浏览量
115 浏览量
2023-04-05 上传
474 浏览量
219 浏览量
172 浏览量
216 浏览量
mayuanjun258
- 粉丝: 0
最新资源
- iOS ZPDatePicker:定制多种时间选择样式
- 控制台进度条的简易实现与测试
- 智能机票查询系统:一键检索国内外航班
- WinSetupFromUSB制作U盘安装WinXp系统教程
- Heig-VD AMT项目1: 构建REST-API的软件即服务平台
- Vue项目轻松集成Hotjar:vue-hotjar NPM包解析
- 2018世界杯足球赛的CRX插件解析
- 打造自定义Android底部弹窗:PicPopupWindow组件的使用
- YOLOv3预训练权重模型下载指南
- Smalltalk Blink项目:创新课程管理系统实践
- 基于JSP MVC的在线图片管理系统的实现
- STM32MP157单片机FreeRTOS任务管理实战教程
- 第六组火车票管理系统4.2的UML实训建模分析
- Studio 3T:提升MongoDB工作效率的终极工具
- 2020年编程挑战:Advent of Code 2020解析
- Android RecyclerView条目选中功能实现示例