掌握高级数据结构：平衡二叉树、优先队列与线段树实例

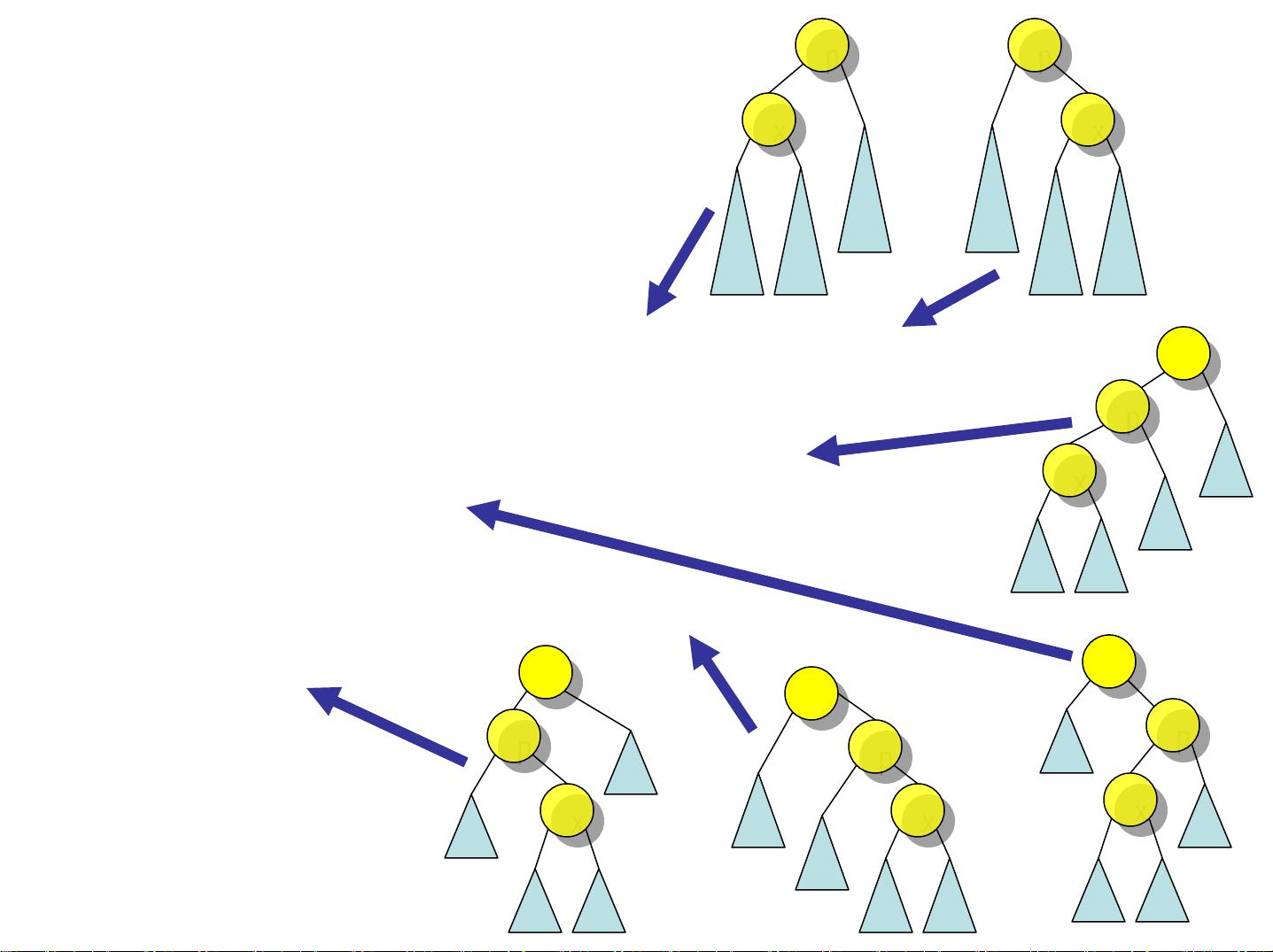
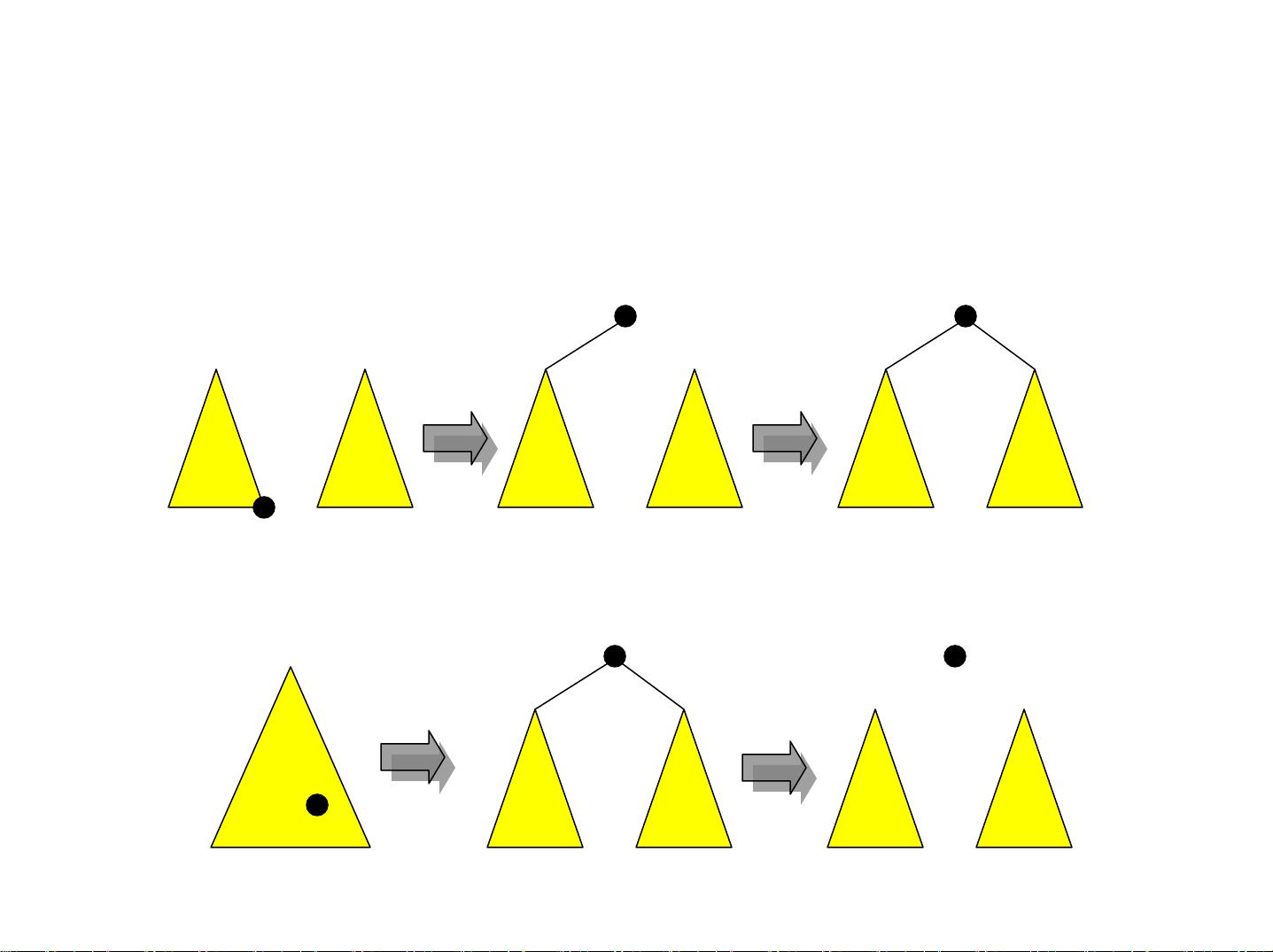
高级数据结构理论和实例深入探讨了高级数据结构在IT领域的核心概念和应用。本课程由刘汝佳主讲，主要内容涵盖了平衡二叉树、可并优先队列、线段树和树状数组，以及最短路径问题的解决方案—— RMQ（Range Minimum Query）和最近公共祖先问题（LCA）。 首先，课程从平衡二叉树开始，这是基本的数据结构，它具有每个节点的左子树小于根节点小于右子树的性质。二叉搜索树（BST）是最简单的平衡二叉树，其操作如查找、插入和删除的时间复杂度通常为O(h)，其中h表示树的高度。然而，为了提高效率，我们追求树的“平衡”，即高度接近对数级增长，这样可以确保操作时间稳定。AVL树是一种严格平衡的二叉搜索树，每个节点的左右子树高度差不超过1，这保证了在固定结点数情况下，树的高度最优。 AVL树的维护通过旋转操作来保持平衡，包括单旋转和双旋转。单旋转用于处理某个子树高度过大时的情况，而双旋转则是当祖父和孙子节点共线或不共线时，对树进行调整。插入新元素时，算法会找到第一个导致不平衡的祖父节点，通过旋转来恢复平衡。 接着，课程介绍了可并优先队列，这是一种特殊的数据结构，能够支持快速的插入和删除操作，并且同时保证元素的优先级关系。这在许多算法和数据结构问题中扮演着重要角色，如Dijkstra算法中的优先队列。 线段树和树状数组是两种高效的数据结构，用于处理区间查询问题。线段树是一颗完全二叉树，可以快速地进行区间求和、最小值等操作；而树状数组则通过压缩和索引计算，提供对区间查询的高效支持。 最后，讲解了Range Minimum Query (RMQ)和最近公共祖先问题(LCA)。RMQ允许在常数时间内查找一个区间内的最小值，这对于图形和动态规划问题中的路径优化至关重要。而LCA问题则涉及寻找两个节点在树中的最近共同祖先，它是许多树形问题的基础，例如在图的路径问题中确定最近的共享祖先节点。 这门课程将高级数据结构的核心原理、实现方法以及实际应用场景紧密结合，对于提升IT专业人士的数据结构理解和应用能力具有重要意义。