数据与算法：图的理论及应用探索

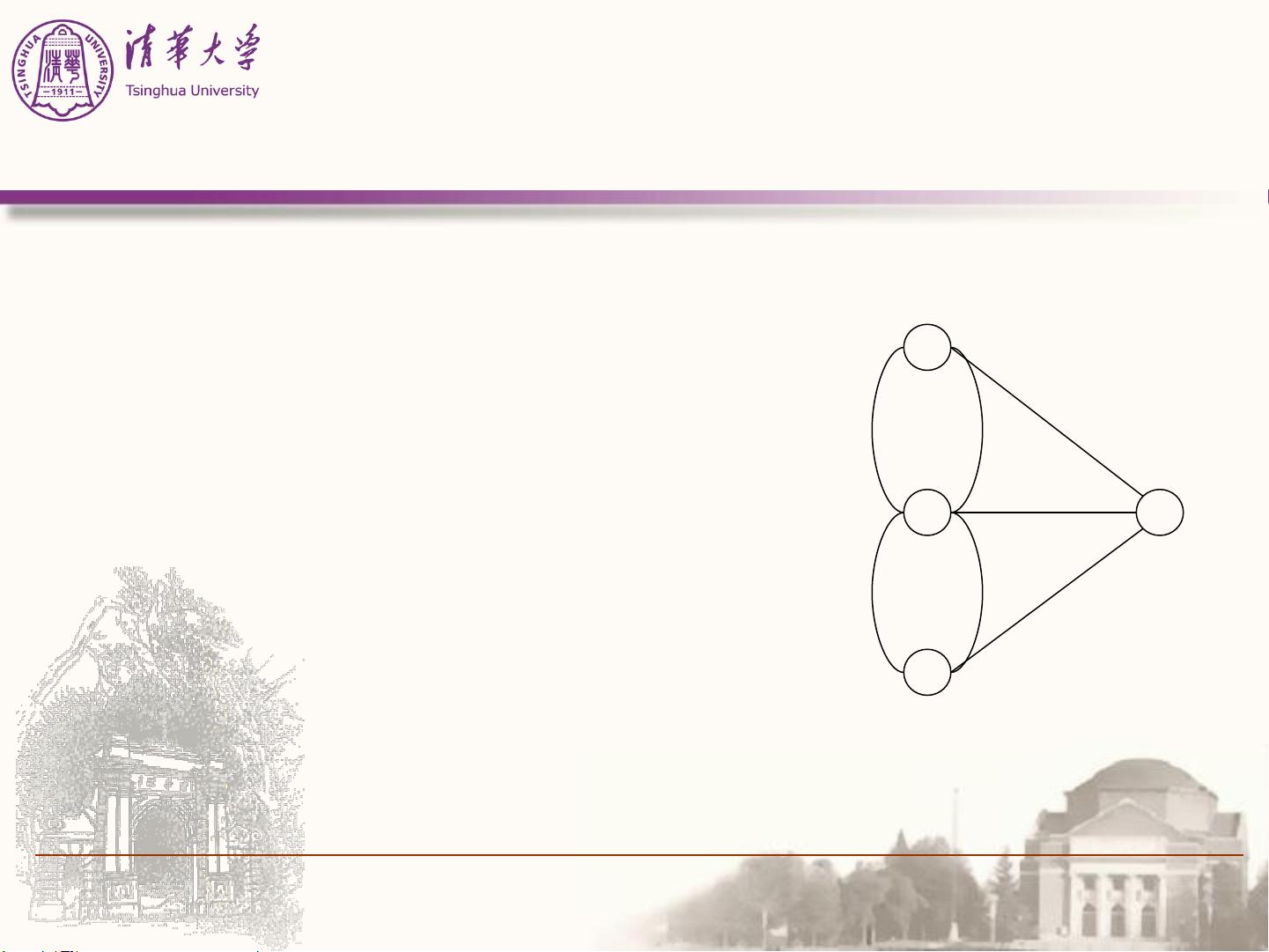
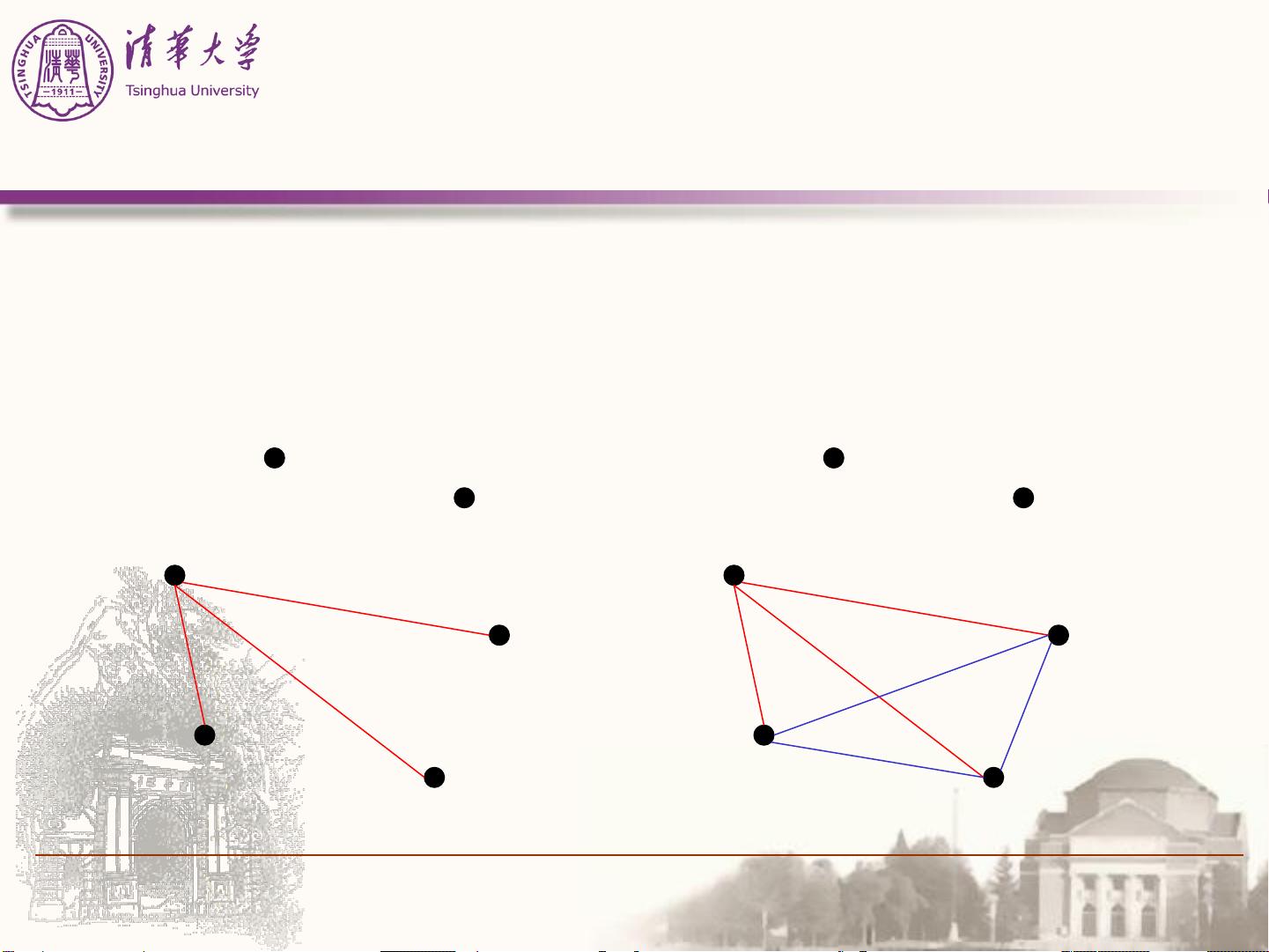
"数据与算法：2基本数据结构8-图.pdf" 本文主要涵盖了数据结构中的图这一重要概念，由吴及在电子工程系所著。文章深入浅出地介绍了图的相关理论及其应用，包括图的基本定义、存储方式、遍历算法、最小生成树和最短路径等核心内容。 首先，文章通过柯尼斯堡七桥问题引出了欧拉路径的概念，这是图论中的一个经典问题。瑞士数学家欧拉研究的这个问题，实质上是在探讨一个图是否存在欧拉路径——即从图中某一点出发，沿着边行走，每条边恰好通过一次并回到起点的路径。这个问题后来被抽象为图论中的"一笔画"问题，对图的性质和遍历算法有着重要意义。 接着，文章详细定义了图的数学形式，一个图G由顶点集V和边集E组成，其中边可以是有向或无向。顶点是图的基本单元，而边则表示顶点之间的关系。有向图的边具有方向，而无向图的边没有方向。此外，文章还讨论了完全图的概念，即在n个顶点的图中，每两个不同的顶点间都有一条边。当边数较少时，这样的图被称为稀疏图；反之，如果边数较多，称为稠密图。 在图的存储方面，文章可能涉及链式存储和邻接矩阵两种常见方式。链式存储通常用于稀疏图，通过邻接表来表示每个顶点的邻接顶点；而邻接矩阵则适合表示任何类型的图，它是一个二维数组，矩阵中的每个元素表示对应顶点之间是否存在边。 接下来，文章可能会讲解图的遍历算法，如深度优先搜索（DFS）和广度优先搜索（BFS）。DFS通常从一个顶点开始，沿着边尽可能深地探索图的分支，直到回溯到没有未访问过的边为止；而BFS则是从一个顶点开始，逐层地访问其所有相邻顶点，直至遍历整个图。 此外，文章还会介绍图的一些关键应用算法，比如最小生成树（Minimum Spanning Tree, MST）问题，常见的解决方法有Prim算法和Kruskal算法，它们用于找到一个连通图中权值最小的边集，这些边构成的树覆盖了图的所有顶点。另一类问题是寻找最短路径，Dijkstra算法和Floyd-Warshall算法是解决这类问题的常用工具。 这份资料详细介绍了图的基本概念、存储结构、遍历算法以及在解决实际问题中的应用，对于理解数据结构和算法，尤其是图论部分，具有很高的学习价值。无论是计算机科学的学生还是专业的软件工程师，都能从中受益匪浅。