控制系统数学模型深入解析：微分方程与传递函数

"自控原理总复习" 在自动控制领域，理解并掌握系统的数学模型是至关重要的，因为它们是分析和设计控制系统的基础。本部分主要涉及三个方面：微分方程、传递函数和频率特性。 微分方程是描述控制系统动态行为的基本工具。在列写系统微分方程时，通常遵循以下五个步骤： 1. 确定系统输入和输出，这可能是物理量如力、速度、位置或电信号。 2. 根据相关的物理定律（如牛顿第二定律）或化学定律，列出所有组成元件的原始方程。 3. 对这些方程进行简化，可能包括忽略次要因素或进行线性化处理，以便于分析。 4. 通过消除中间变量，从输入端开始，按照信号传递顺序组合这些方程，得到输入与输出之间的微分方程。 5. 对微分方程进行标准化，使输出项在等号左侧，输入项在右侧，并排列成降幂形式，同时将系数调整为具有物理意义的形式。 以弹簧-质量-阻尼器系统为例，当质量m受到外力F(t)作用时，可以利用牛顿第二定律列出微分方程。考虑阻尼器的阻尼力F1(t)和弹簧的弹性力F2(t)，经过整理，我们得到描述该系统运动的微分方程： m * d²x(t)/dt² + f * dx(t)/dt + K * x(t) = F(t) 这里，m是质量，f是阻尼系数，K是弹性系数，x(t)是位移，dx(t)/dt是速度，d²x(t)/dt²是加速度。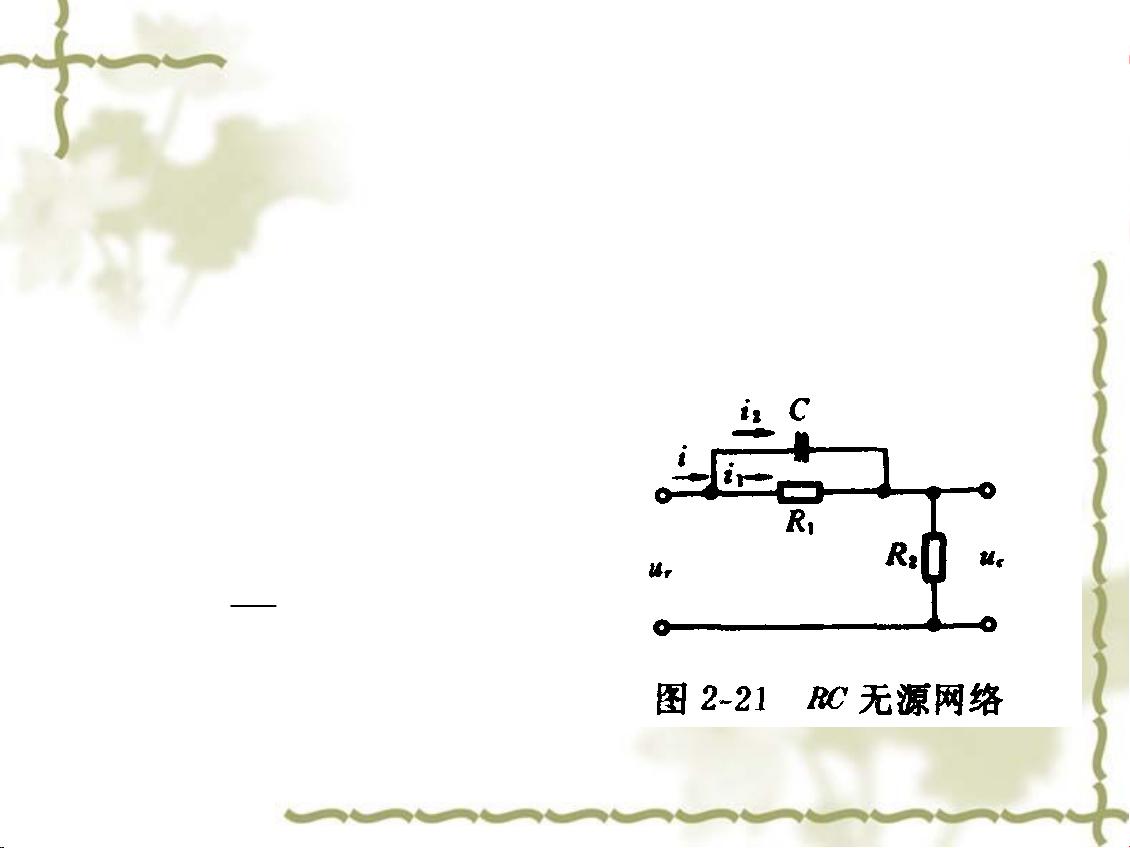 另一个例子是RC滤波网络，它是一个常见的电子电路。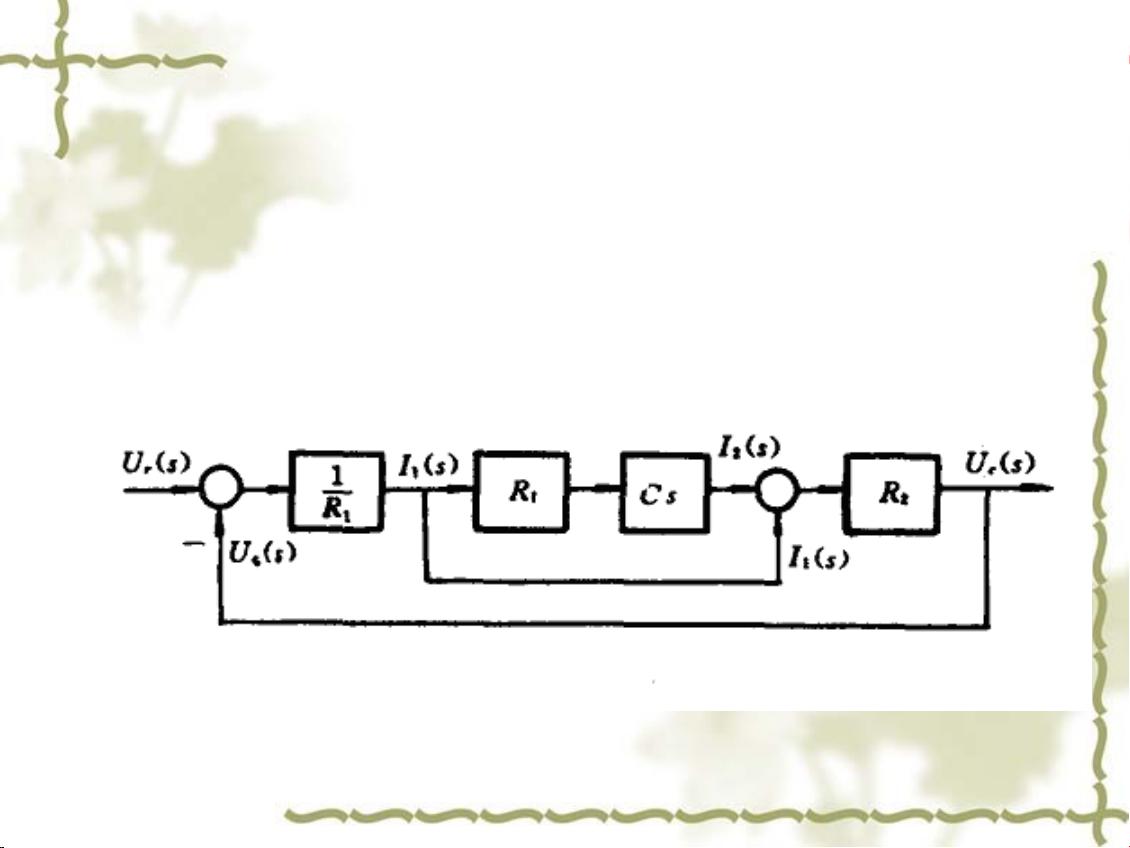通过应用基尔霍夫电压定律，我们可以消除中间变量电流i1和i2，得到关于输入电压Ur(t)和输出电压Uc(t)的微分方程： R1*C1*dUc(t)/dt + R2*C2*(d²Uc(t)/dt²) = Ur(t) - Uc(t) 传递函数是线性定常系统的重要概念，特别是在零初始条件下。它是系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。对于上面的RC滤波网络，可以通过对微分方程进行拉普拉斯变换来求得其传递函数，这有助于分析系统的频率响应和稳定性。 频率特性则揭示了系统在不同频率输入下的响应。通过绘制波特图，我们可以直观地了解系统的增益和相位变化，这对于设计滤波器、控制器等至关重要。频率特性分析通常包括幅频特性和相频特性，它们可以帮助我们了解系统在高频和低频输入下的性能。 自控原理中的微分方程、传递函数和频率特性是理解系统动态行为和设计控制策略的基础。掌握这些概念和工具，能帮助工程师有效地分析和优化各种控制系统。