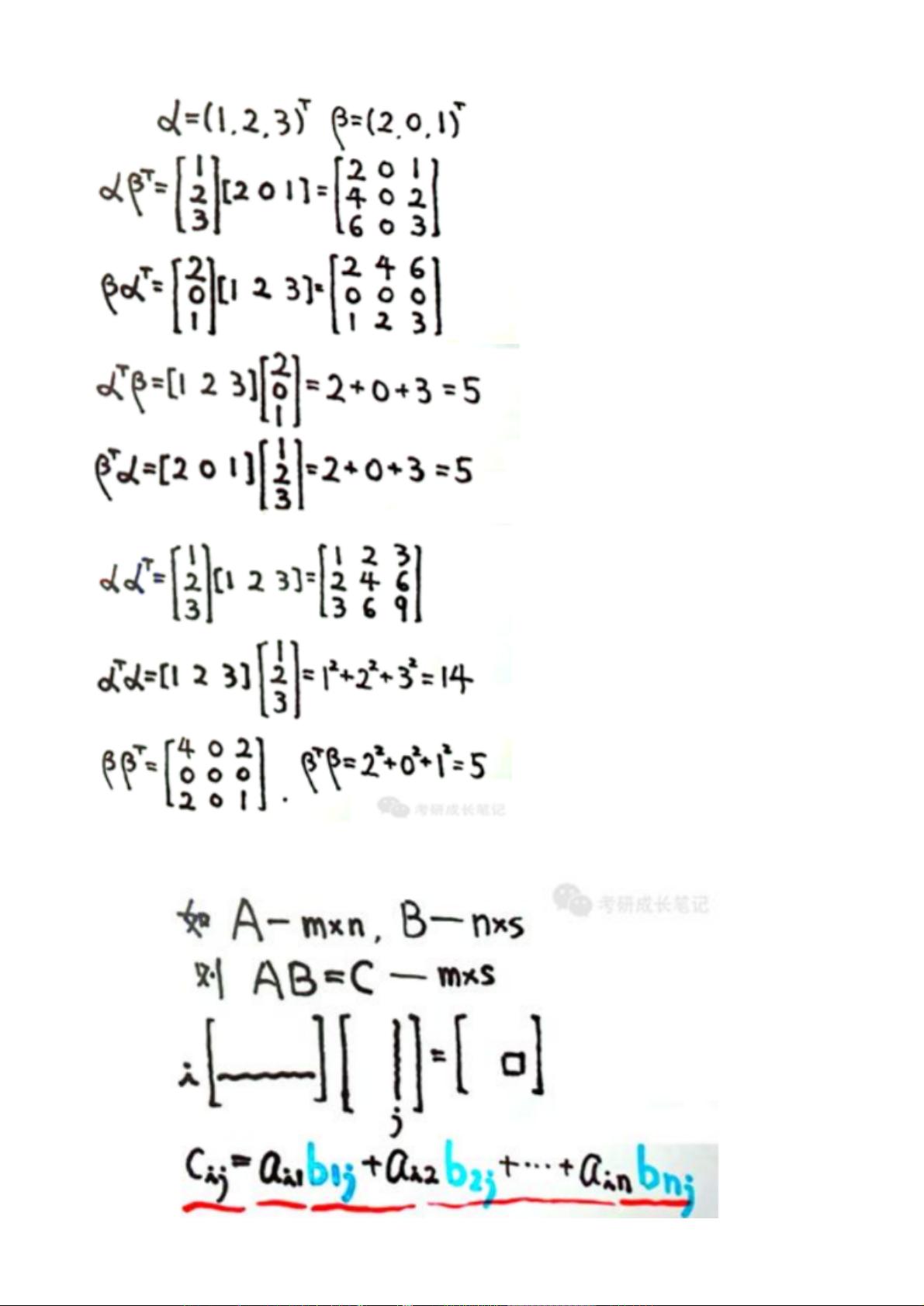线性代数笔记：行列式计算与性质解析

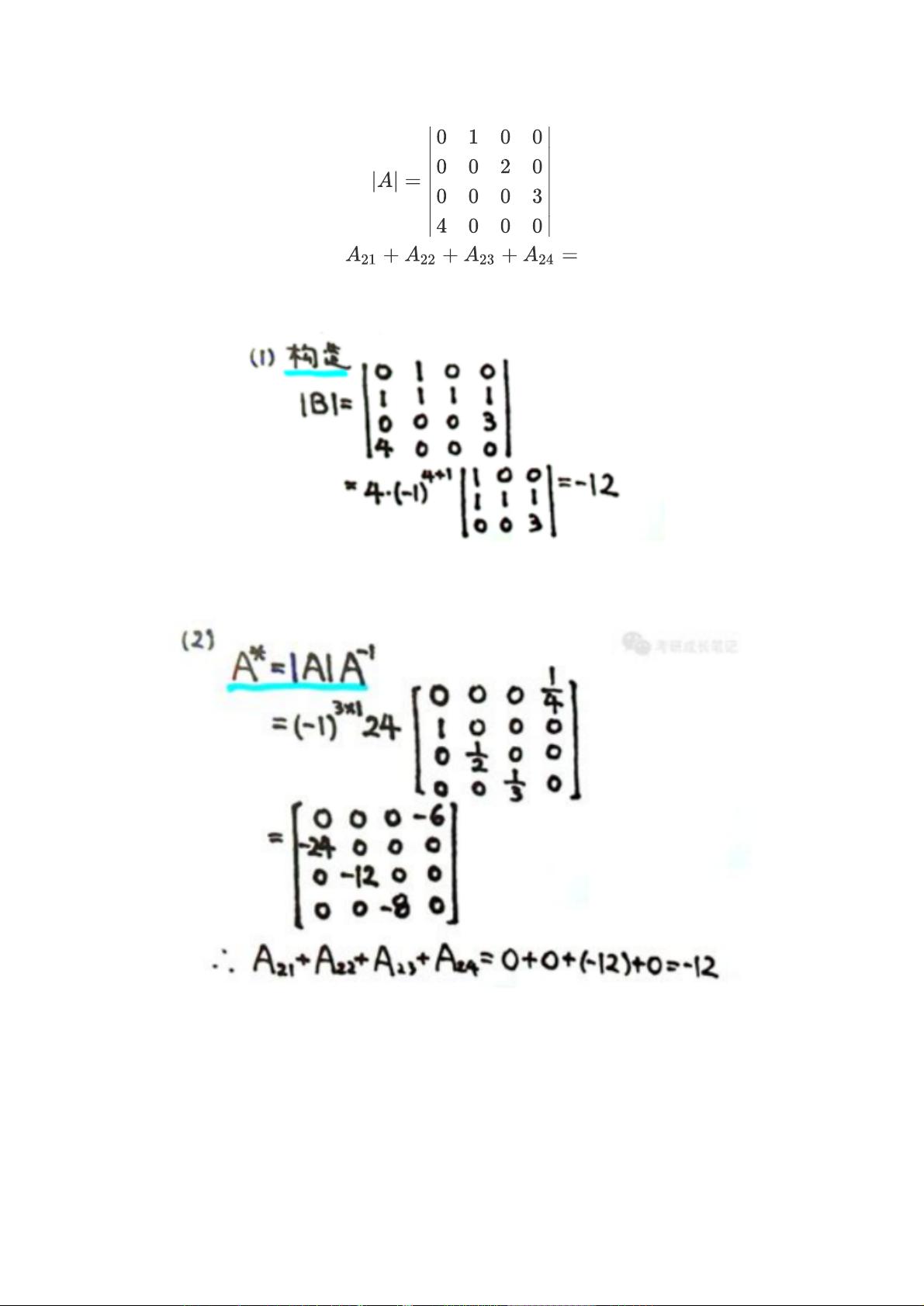
"这是一份2020考研线性代数强化课程的笔记，主要涵盖了行列式的计算、性质及应用，以及与矩阵相关的概念，包括余子式、代数余子式、矩阵的初等变换和行列式的计算方法。笔记强调了行列式与矩阵的区别，并介绍了拉普拉斯展开、范德蒙行列式、爪型行列式和数学归纳法在求解行列式中的应用。此外，还涉及到了矩阵的特征值、相似变换和逆矩阵等相关知识。" 在《线性代数》的学习中，行列式是核心概念之一。行列式既不是矩阵本身，而是一种特殊的数值，它反映了矩阵的一些本质属性。行列式的计算主要包括数字型和抽象型两种类型。数字型行列式通常较为直观，而抽象型行列式则涉及更多的理论计算。行列式的性质包括：某行元素的线性组合并不改变行列式的值，这一性质常用于简化计算。 余子式和代数余子式是理解行列式性质的基础。余子式是通过在原始行列式中删除一行一列后得到的小型行列式，而代数余子式则是余子式乘以该位置元素的符号（奇数位置为负，偶数位置为正）。掌握这两个概念有助于理解行列式的性质和展开公式。 行列式的5个重要性质是解题的关键，比如某行的所有元素是两个数之和时，行列式可分解为两部分；某行的k倍加到另一行，行列式不变。这些性质在进行行列式计算时十分实用，特别是拉普拉斯展开和范德蒙行列式公式，它们提供了解决行列式问题的有效途径。 在解决抽象型行列式时，数学归纳法是求解n阶行列式的一种方法，分为第一数学归纳法和第二数学归纳法。数学归纳法能够处理复杂的递推关系，帮助我们逐步建立解题思路。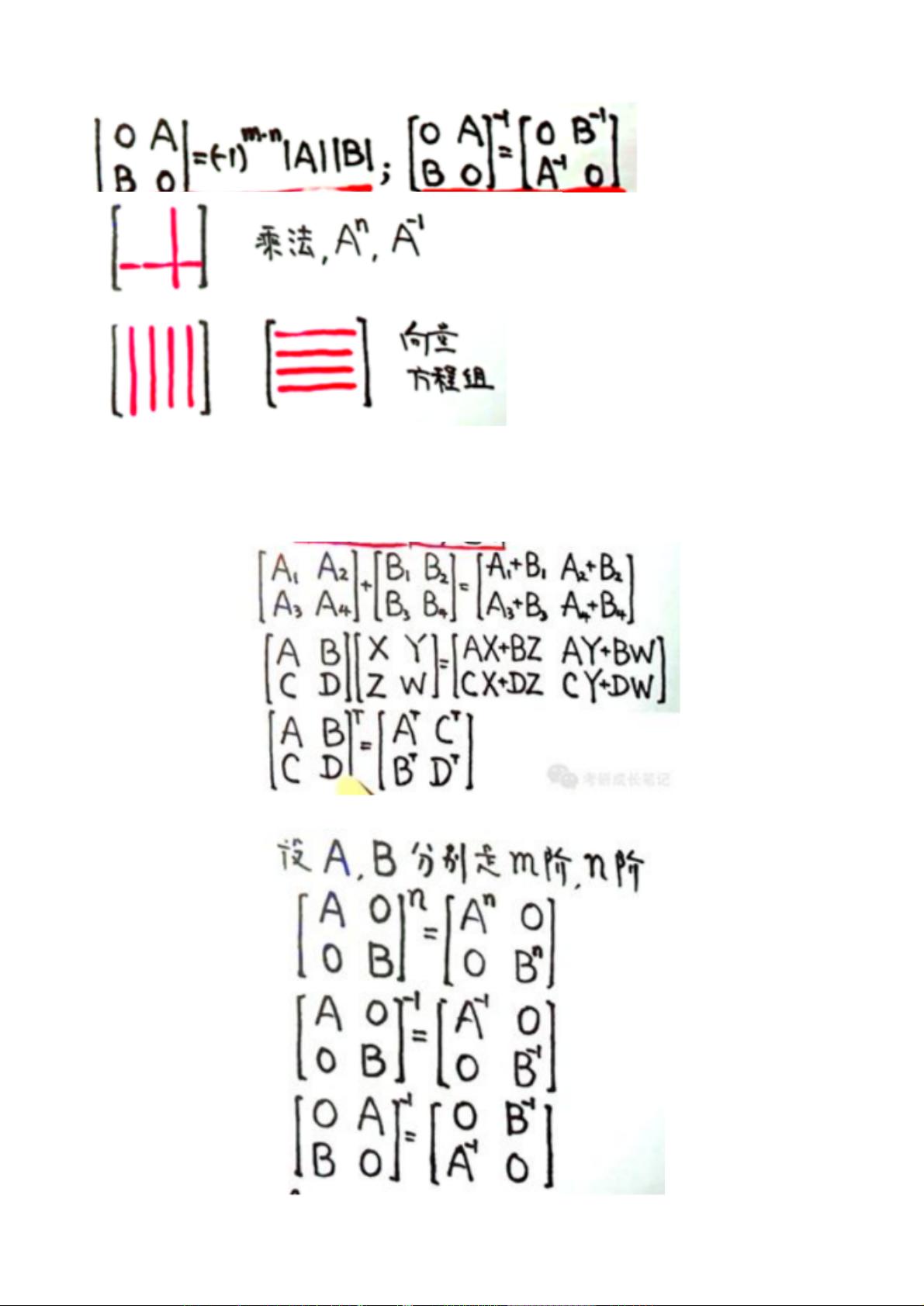 爪型行列式是一种特定形式的行列式，它的特点是某些行或列具有共同的元素，处理这类问题时，可以通过特殊的方法简化计算。此外，矩阵的和、逆、伴随以及特征值和相似性是线性代数的另一个重要部分。对于矩阵的和，其行列式等于各矩阵行列式的和；而矩阵的逆和伴随则涉及到矩阵运算的深入理解，特征值和相似性则揭示了矩阵的结构特性。 在解题实践中，灵活运用各种方法，例如恒等变形、逐行相加、拉普拉斯展开等，可以帮助我们有效地计算行列式。同时，对于抽象型的行列式题目，尝试多种解题策略能加深对定理和公式的理解。 这份笔记全面覆盖了线性代数的基础知识，特别针对考研复习提供了强化学习的路径，帮助学生巩固理论基础，提升解题能力。