掌握图论基础：存储、遍历与关键算法

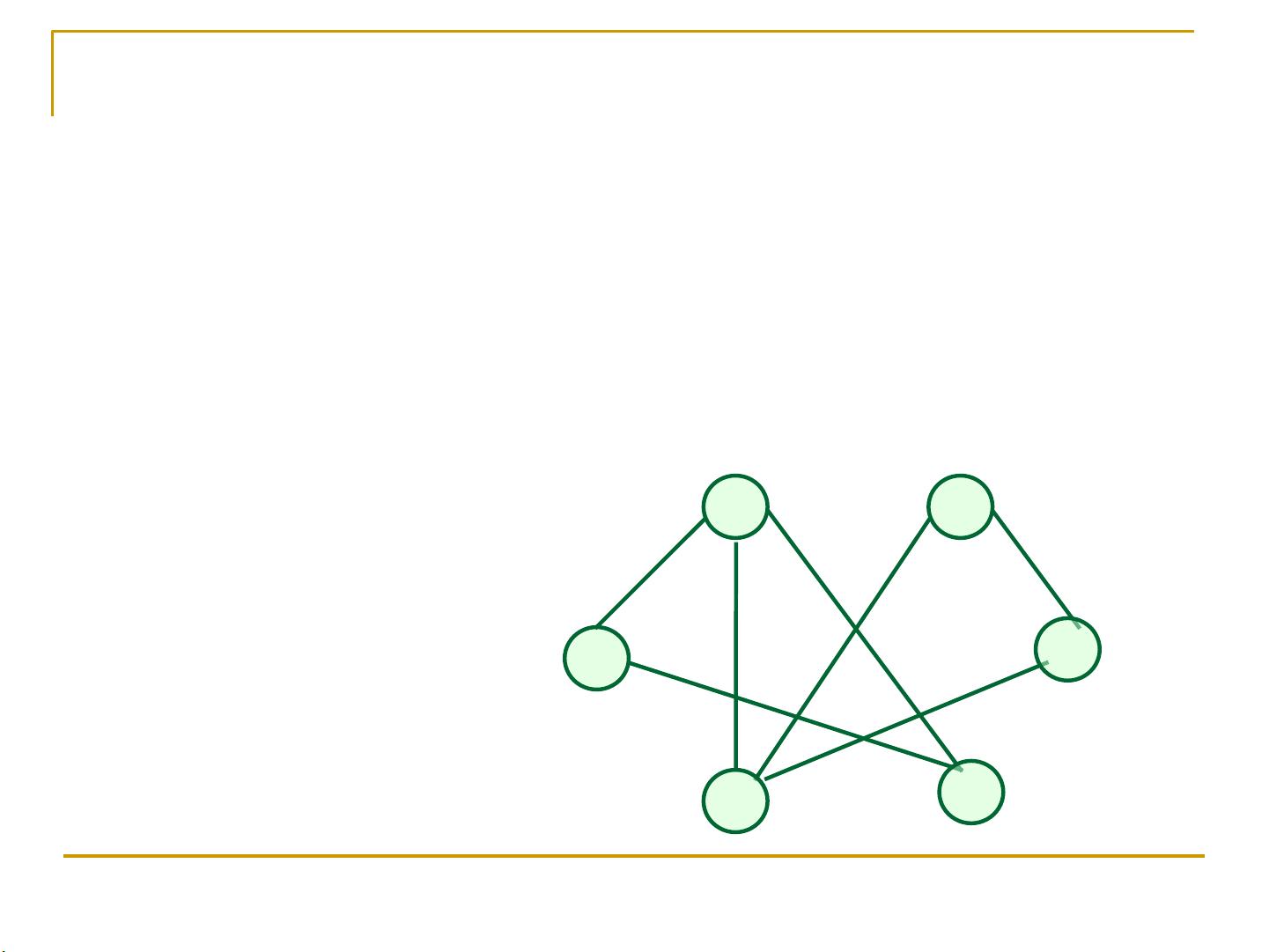
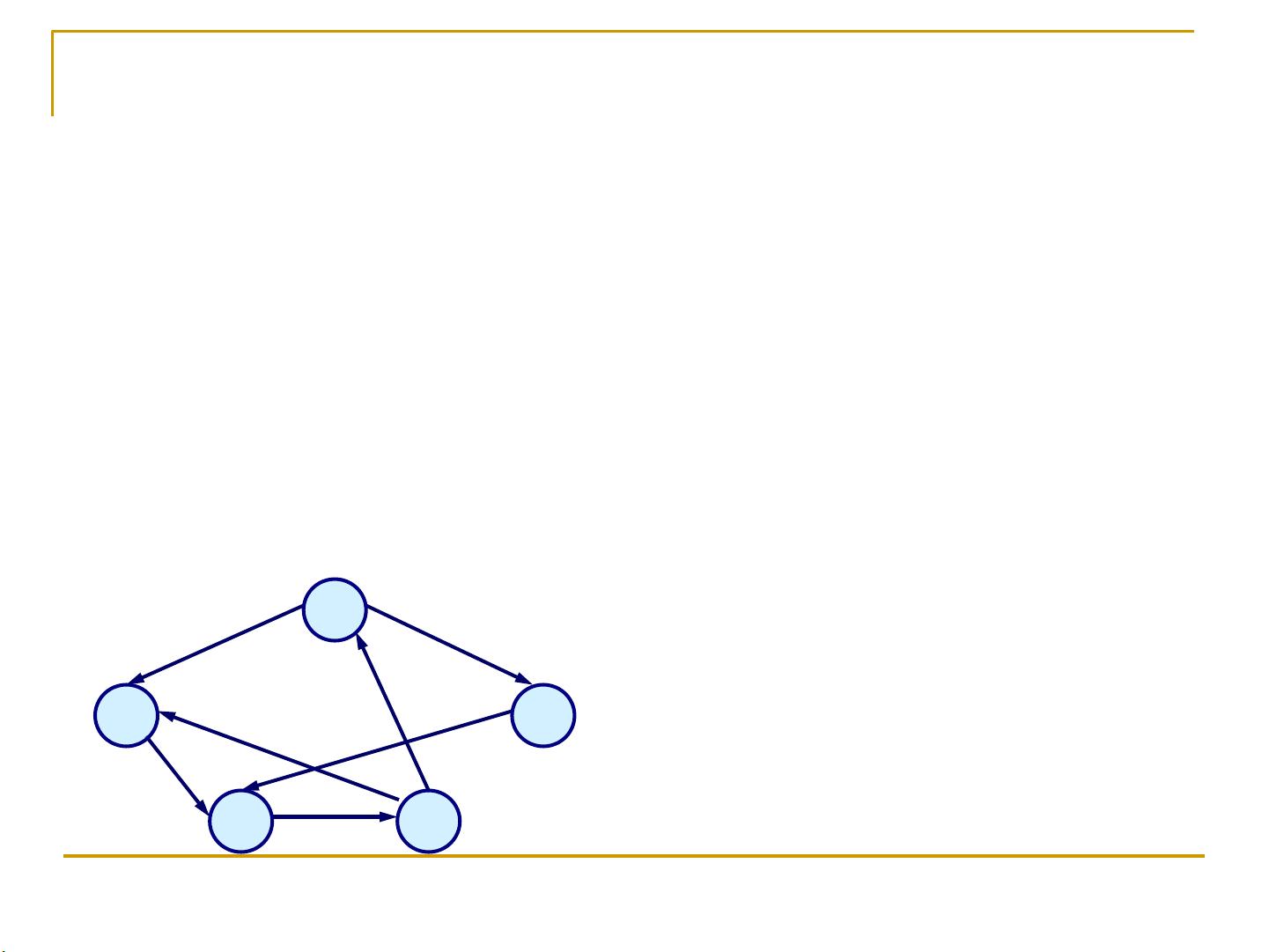
在第七章《图》中，我们深入探讨了图这一重要的数据结构在计算机科学中的应用。首先，本章的主要目标包括熟悉图中基本的术语和概念，如顶点、弧、有向图与无向图的区别，以及边的定义。图被抽象定义为由顶点集V和弧集VR组成的结构，<v,w>表示从v到w的弧，其方向性使得图可以分为有向图和无向图。 在存储表示方面，我们重点学习了图的两种常见方式：邻接矩阵和邻接表。邻接矩阵是用二维数组表示图，每个元素对应一对顶点，值表示它们之间是否有边；而邻接表则是使用链表来存储每顶点的相邻顶点，空间效率较高，适用于稀疏图。 遍历图是理解图的重要步骤，包括深度优先搜索(DFS)和广度优先搜索(BFS)。DFS从一个顶点出发，尽可能深地探索分支，直到达到叶子节点；而BFS则是从根节点开始，按层次顺序依次访问每个节点。这两种方法在解决实际问题中都有广泛应用。 接下来，章节介绍了最小生成树(MST)的概念，它是图中连接所有顶点且边权总和最小的树。常用算法如Prim算法和Kruskal算法用于求解最小生成树。此外，我们还会学习如何进行拓扑排序，这是一种对有向无环图(DAG)中顶点进行排序的方法，它确保了所有依赖关系都满足。 关键路径是图中决定项目完成时间最长的路径，对于项目管理等场景非常重要。通过找出关键路径，我们可以了解项目中最短的时间窗口和可能的风险。 在本章的最后部分，讨论了两点之间的最短路径问题，特别是Dijkstra算法和Floyd-Warshall算法，它们分别适用于带权重的有向图和无向图，用来找到两个顶点之间的最短路径。 第七章全面覆盖了图的基础理论、存储、遍历算法、优化问题以及实际应用，是理解图论及其在信息技术领域核心作用的关键篇章。