利用Python实现逻辑回归：预测大学录取

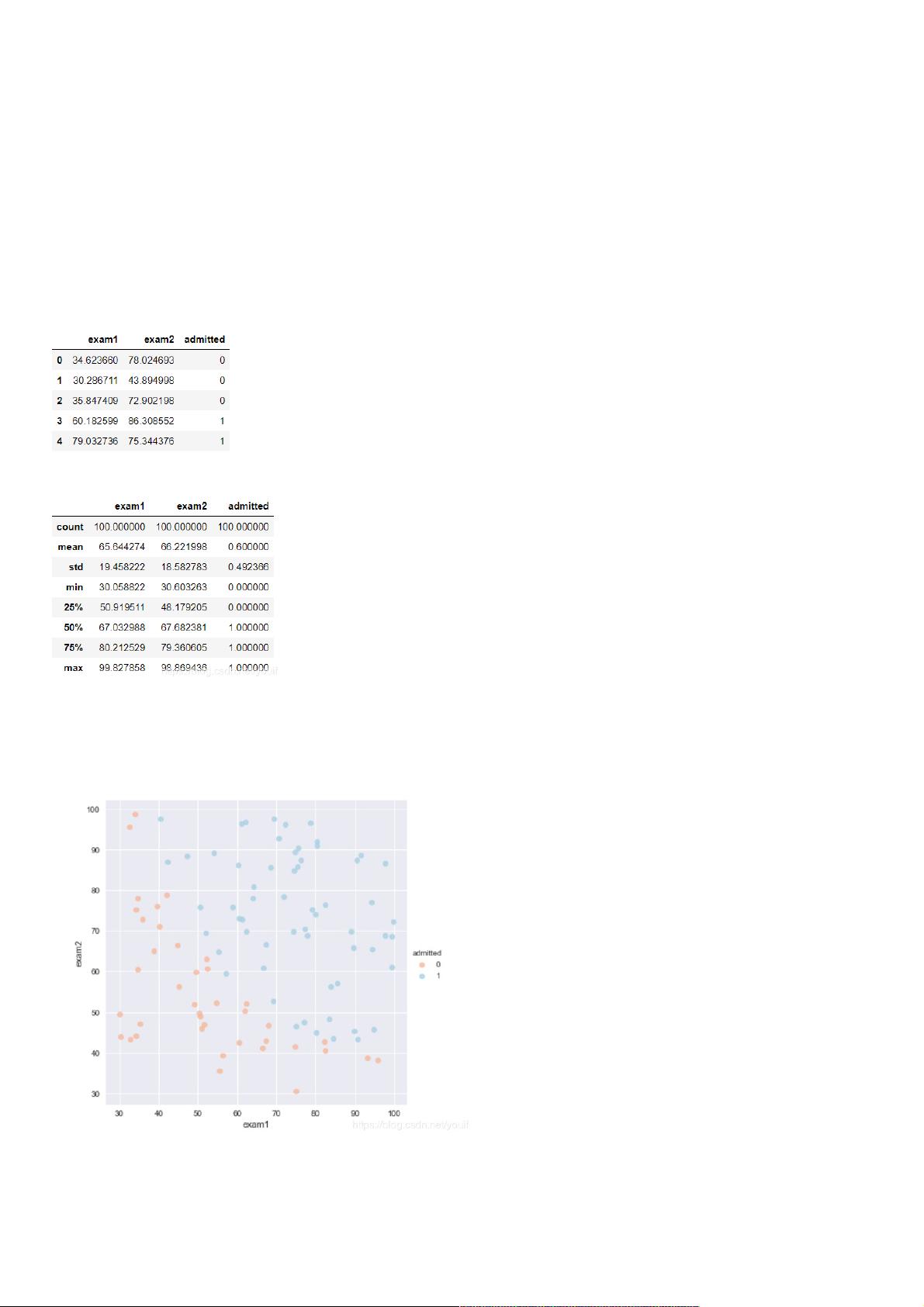
在编程作业2中，吴恩达教授指导我们学习和实践逻辑回归（Logistic Regression）这一概念，这是一种在二分类问题中常用的统计模型。作业的目标是使用Python 3.6环境构建一个逻辑回归模型，预测一个学生被大学录取的可能性，依据两个考试成绩（'Exam1'和'Exam2'）作为输入特征。 首先，准备工作至关重要，我们通过`pandas`库读取名为'ex2data1.txt'的数据集，该数据包含了申请人的考试成绩以及他们是否被录取的信息。通过`head()`函数查看前五行数据，并利用`describe()`了解数据的统计特性。在这个阶段，可能遇到错误，比如当尝试使用`seaborn`库中的颜色时，因为`_ColorPalette`对象不可哈希，解决方法是调整`seaborn`的设置，如使用`"notebook"`风格和自定义画板颜色。 接下来，作业涉及的主要概念包括： 1. **Sigmoid函数**：这是一个S型函数，也称作逻辑函数，其输出值范围在0到1之间，常用于将线性函数的结果转换为概率形式，使得结果易于理解和解释。 2. **Cost函数（代价函数）**：逻辑回归的代价函数通常采用交叉熵的形式，衡量模型预测概率与真实标签之间的差异。优化这个函数是通过梯度下降法找到最佳模型参数。 3. **Gradient Descent（梯度下降）**：这是一种迭代优化算法，通过计算成本函数关于参数的梯度（方向），沿着梯度的反方向更新参数，直到找到最小化代价的最优解。在这个作业中，我们需要实现参数的梯度计算和更新过程。 4. **拟合参数（θ0, θ1, θ2）**：这些参数代表了模型对每个特征的权重和截距，是通过最小化代价函数来确定的。在本任务中，目标是求解这三个参数，从而确定录取决策的分界线。 5. **预测和验证**：使用训练集中的数据，通过计算sigmoid函数的结果并设定阈值（通常为0.5）来预测学生的录取情况。然后，我们会计算预测的准确性，评估模型性能。 6. **决策边界**：逻辑回归模型在二维空间中形成的决策边界，它将不同类别的数据分开。通过分析参数，我们可以理解模型如何基于考试成绩区分录取和不录取的申请者。 7. **推导**：这里可能涉及理论上的推导，例如梯度下降算法背后的数学原理，或者sigmoid函数如何与逻辑回归结合。 8. **代码实现**：具体到Python代码层面，涉及到导入必要的库，如`numpy`、`sklearn.metrics`等，以及使用这些库函数来执行上述步骤。比如，`sigmoid`函数的实现、模型预测、`classification_report`的使用等。 编程作业2围绕逻辑回归的核心概念展开，旨在通过实际操作加深对二元分类问题的理解，并掌握机器学习模型训练和评估的关键步骤。完成这个项目后，你将具备使用逻辑回归处理实际问题的能力，并能根据数据调整和优化模型。