深度学习基石：反向传播与计算图微积分解析

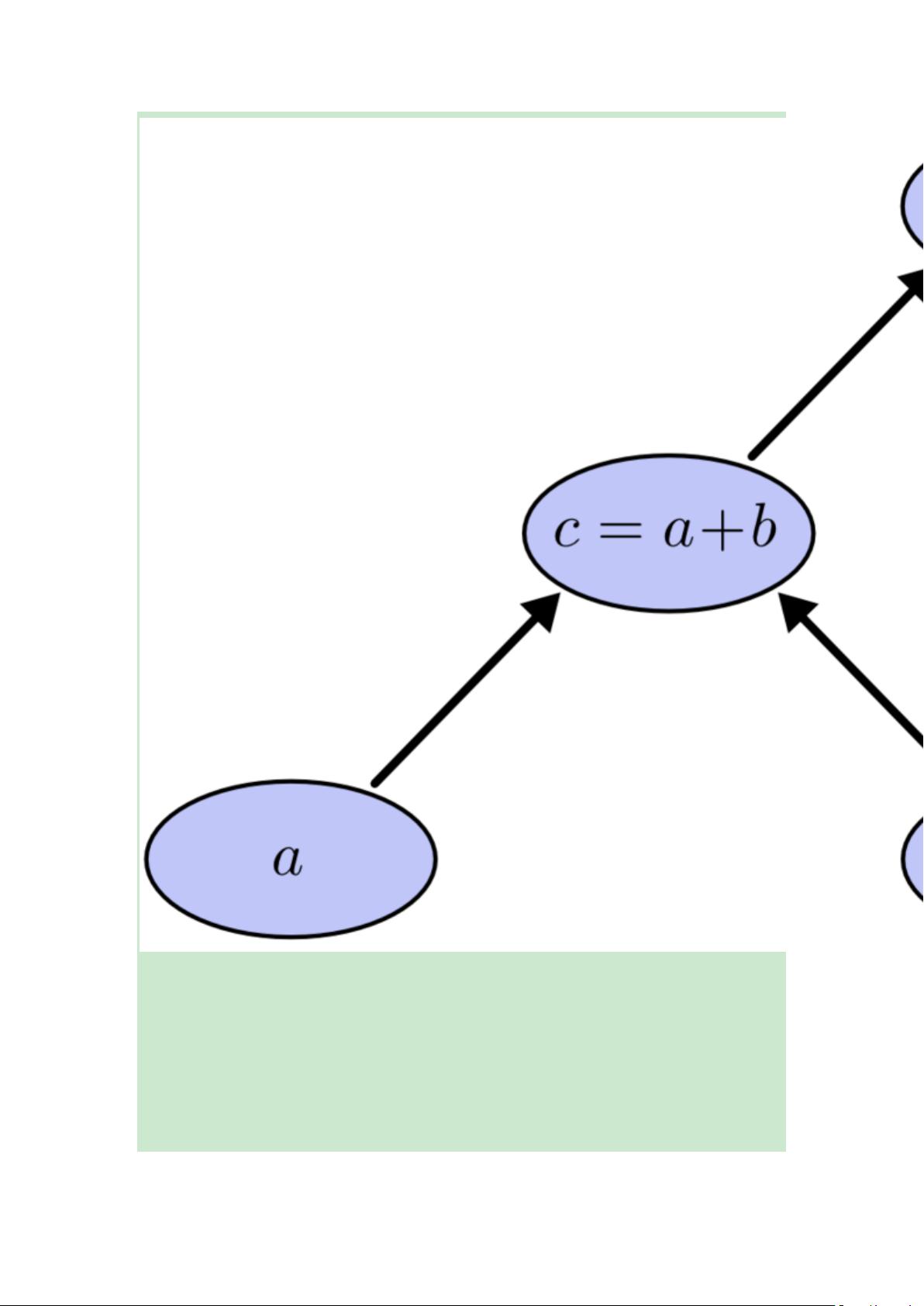
"这篇文章除了介绍计算图上的微积分，特别强调了反向传播算法（Backpropagation）在深度学习中的核心地位，并指出它其实是一种通用的快速求导技术，可应用于广泛的数值计算场景。文章以计算图为例，解释了如何表示数学表达式，并通过计算图来求解表达式的值。接着，文章引入了计算图上的导数概念，特别是边上的导数，即偏导数，这里提到了和式法则和乘式法则作为计算的基础。" 在深入讨论计算图上的微积分之前，我们先要理解什么是计算图。计算图是一种图形表示方法，用于描述一系列计算操作的流程。在这个图中，每个节点代表一个操作或变量，而边则表示操作之间的依赖关系。例如，给定表达式 e = (a + b) * (b + 1)，可以通过计算图将加法和乘法操作以及中间变量可视化。 反向传播是深度学习中用于优化模型参数的关键算法。它利用链式法则，通过计算图从输出反向传播误差，从而有效地计算出每个参数对损失函数的梯度。这个过程大大加速了权重更新的速度，使得深度网络的训练成为可能。 在计算图上，要计算某个变量的偏导数，就需要应用微积分中的基本规则。和式法则表明，如果你有两个项相加，它们对整体的贡献之和就是它们各自的导数之和。乘式法则则指出，两个函数的乘积的导数是这两个函数导数的乘积加上第一个函数的值乘以第二个函数的导数，再减去第二个函数的值乘以第一个函数的导数。 在给出的计算图示例中，每个边上的导数表示的是一个变量对另一个变量的直接影响。例如，如果a直接影响c，那么我们关注的是a变化时c的变化率，即c关于a的偏导数。通过应用和式法则和乘式法则，我们可以沿着计算图的路径计算出任何两个不直接相连的节点之间的偏导数。 总结来说，计算图上的微积分是理解反向传播和深度学习模型训练基础的关键。通过构建计算图，我们可以清晰地看到计算过程，并利用微积分的规则有效地计算导数，这对于优化模型的参数至关重要。计算图不仅限于深度学习，也是其他领域如数值分析中求解复杂问题的有力工具。