"计算机算法设计与分析：Chp15-动态规划1"

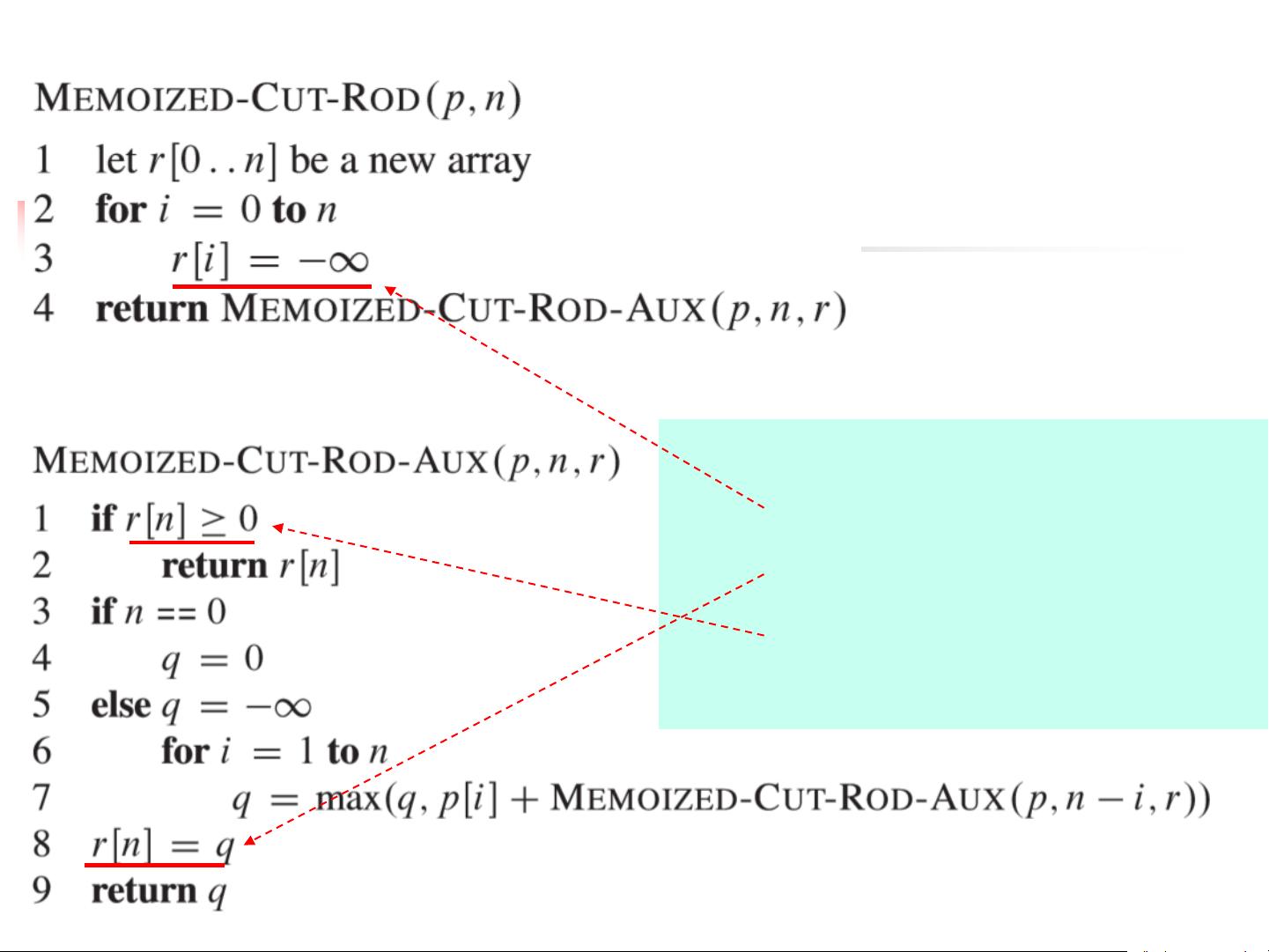
动态规划是一种用于解决优化问题的算法设计与分析方法。在动态规划的过程中，我们会刻画一个最优解的结构特征，递归地定义最优解的值，并计算最优解的值，最终利用计算出的信息来构造一个最优解。本文将对动态规划进行详细的探讨，介绍其基本原理和算法设计与分析。 首先，让我们来了解动态规划的基本原理。动态规划是一种通过将问题分解成相互重叠的子问题来解决问题的方法。在动态规划中，我们会寻找最优解的结构特征，这些特征能够帮助我们找到最优解的全局性质。通过递归地定义最优解的值，我们能够得到问题的最优解，以及该最优解是如何由问题的子问题构成的。接着，我们会计算最优解的值，这一步骤通常需要使用递归或迭代的方法来进行求解。最后，我们利用计算出的信息来构造一个最优解，这一步通常需要使用一些额外的数据结构来辅助构建最优解。 在动态规划的过程中，我们需要注意一些基本原则。首先，我们需要明确问题的最优子结构性质，这里指的是问题的一个最优解包含其子问题的最优解。其次，我们需要进行重叠子问题的处理，即对于问题中重复出现的子问题，我们需要进行记忆化处理，以避免重复计算。最后，我们需要设计一个合适的状态转移方程，以便正确地递归地定义最优解的值。在实际应用中，我们需要根据具体问题的特性来设计和分析算法，以保证算法的正确性和高效性。 动态规划在计算机算法设计中有着广泛的应用。例如，在图论中，动态规划可以用来解决最短路径和最小生成树等问题；在字符串处理中，动态规划可以用来解决最长公共子序列和编辑距离等问题；在背包问题中，动态规划可以用来解决0-1背包和多重背包等问题。通过动态规划的算法设计与分析，我们能够有效地解决这些优化问题，得到最优的解决方案。 在总结上述内容时，我们发现，动态规划是一种重要的算法设计与分析方法，它通过刻画最优解的结构特征、递归地定义最优解的值、计算最优解的值，并利用计算出的信息构造一个最优解来解决优化问题。在应用动态规划时，我们需要注意问题的最优子结构性质、重叠子问题的处理、状态转移方程的设计等基本原则。通过动态规划的算法设计与分析，我们能够解决各种优化问题，得到最优的解决方案。因此，动态规划是一种非常重要和实用的算法设计与分析方法，值得我们深入学习和研究。