图形模型入门：概率论与图论的结合在机器学习中的应用

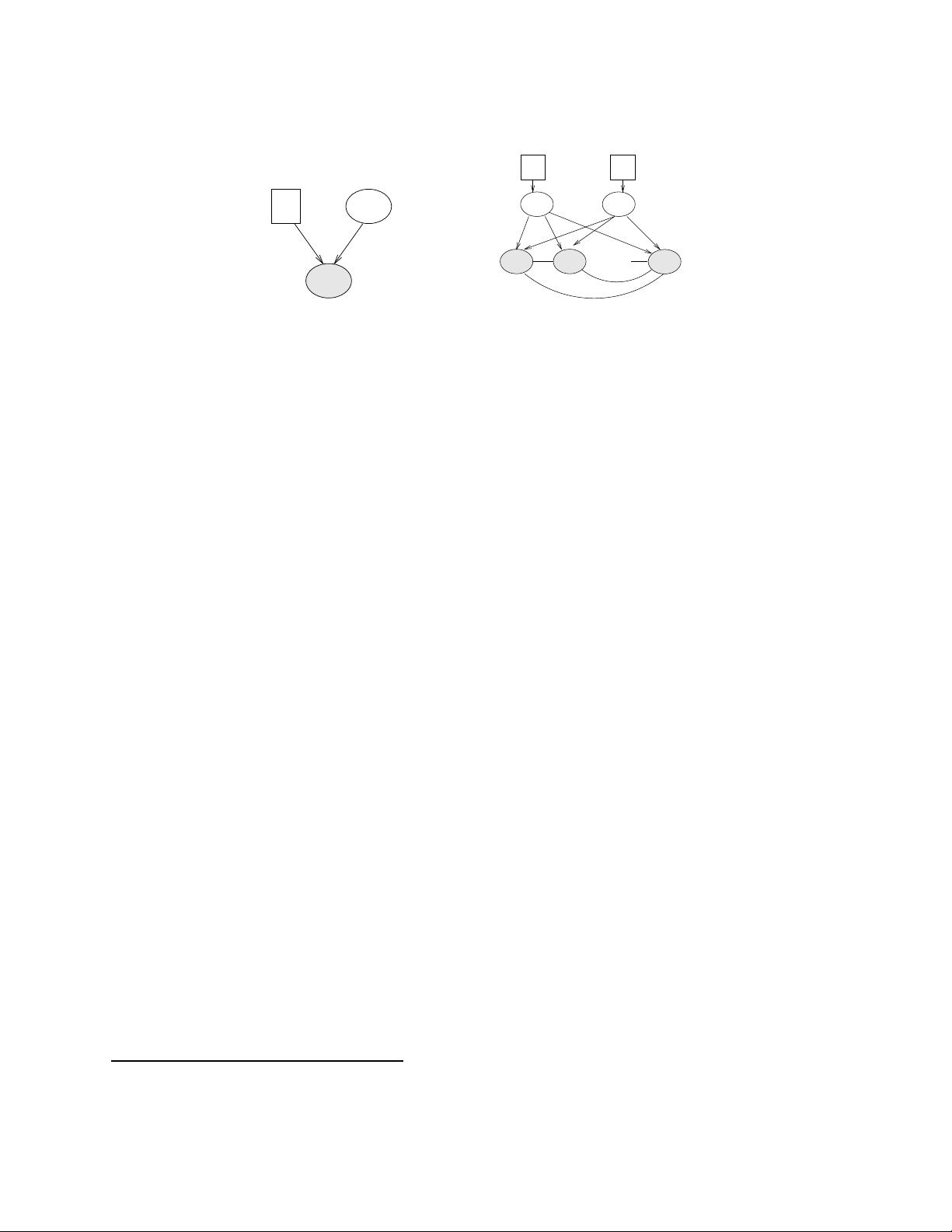
"An introduction to graphical models" 图模型是概率论与图论的结合，它提供了解决应用数学和工程领域普遍存在的不确定性和复杂性问题的自然工具，特别是在机器学习算法的设计和分析中扮演着越来越重要的角色。图模型的核心概念是模块化，即通过组合更简单的部分来构建复杂的系统。概率论作为粘合剂，确保了系统的整体一致性，并提供了将模型与数据对接的方法。图论的方面为人类提供了一种直观的方式来建模高度交互的变量集，同时也为设计高效的一般目的算法提供了天然的数据结构。 图模型的基本构成包括节点（nodes）和边（edges）。节点通常代表随机变量，而边则表示这些变量之间的相互依赖关系。根据边的方向和存在与否，图模型可以分为两大类：有向图模型（Directed Graphical Models，如贝叶斯网络）和无向图模型（Undirected Graphical Models，如马尔可夫随机场）。在有向图中，边的方向指示了变量之间的因果关系，而在无向图中，边的存在表示变量之间的条件独立性。 在机器学习中，图模型被广泛应用于概率推理、特征选择、结构学习和参数估计等任务。例如，在贝叶斯网络中，可以通过利用贝叶斯规则进行条件概率的计算，从而实现不确定性推理。马尔可夫随机场则常用于图像处理和自然语言处理，如图像分割和词性标注，因为它能有效地捕获局部和全局的依赖关系。 图模型的效率主要体现在它们能够利用局部信息来推断整个系统的状态。通过利用图的稀疏性，可以设计出高效算法，如消息传递算法（Message Passing Algorithms），如信念传播（Belief Propagation）和最大似然估计的期望最大化（Expectation-Maximization, EM）算法。 此外，图模型还与统计力学中的多变量概率系统紧密相关，如吉布斯分布（Gibbs distribution）和贝叶斯网络的联合分布。这些理论为理解和处理大量变量间的复杂相互作用提供了框架。例如，在社交网络分析中，图模型可以帮助识别关键人物和群组结构，或者在生物信息学中，可以解析基因表达数据以揭示基因间的相互作用网络。 总结来说，图模型是理论与实践的桥梁，它简化了对复杂系统理解和建模的过程，使得我们能够处理现实世界中的不确定性和复杂性。随着计算能力的增强和大数据时代的到来，图模型在解决各种实际问题中将继续发挥关键作用。