MATLAB实现蒙特卡罗算法详解

"这篇文档是关于使用MATLAB实现蒙特卡罗算法的详细介绍，涵盖了算法的历史、基本原理、以及在数值积分中的应用。" 在MATLAB中实施蒙特卡罗算法，首先要理解其核心思想。蒙特卡罗方法源于概率论和统计学，通过大量随机抽样或试验来解决问题。这种方法的命名来源于摩纳哥的赌博胜地——蒙特卡洛，因为其随机性的特点与赌博中随机事件的性质相呼应。 历史上，蒙特卡罗方法最早可追溯到法国科学家布丰的投针试验，用来估算圆周率π。在现代，这种方法在许多领域都有广泛应用，特别是在那些解析解难以获得或计算成本过高的问题中，如物理、工程、金融和计算机科学。 在MATLAB中，蒙特卡罗方法常用于数值积分。当面对复杂的函数f(x)，我们无法找到原函数F(x)进行直接积分时，蒙特卡罗方法提供了一种有效且直观的解决方案。传统的数值积分方法如辛普森法则、梯形法则等，会通过将区间细分并计算各小段的近似积分来逼近真实值。然而，这些方法需要对每一段进行精确计算，而蒙特卡罗方法则更为简洁。 在MATLAB中实现蒙特卡罗数值积分，步骤如下： 1. **定义积分区间**：设定积分的上下限x0和x1。 2. **生成随机样本**：在区间[x0, x1]内生成大量随机数x，这可以通过MATLAB的`rand`函数实现。 3. **计算函数值**：对于每一个随机数x，计算对应的函数值f(x)。 4. **统计计算**：统计落在积分区域下方的样本点比例P，即函数值f(x)小于或等于零的比例。 5. **计算积分近似值**：利用公式`I ≈ (x1 - x0) * P`，其中I是积分的近似值。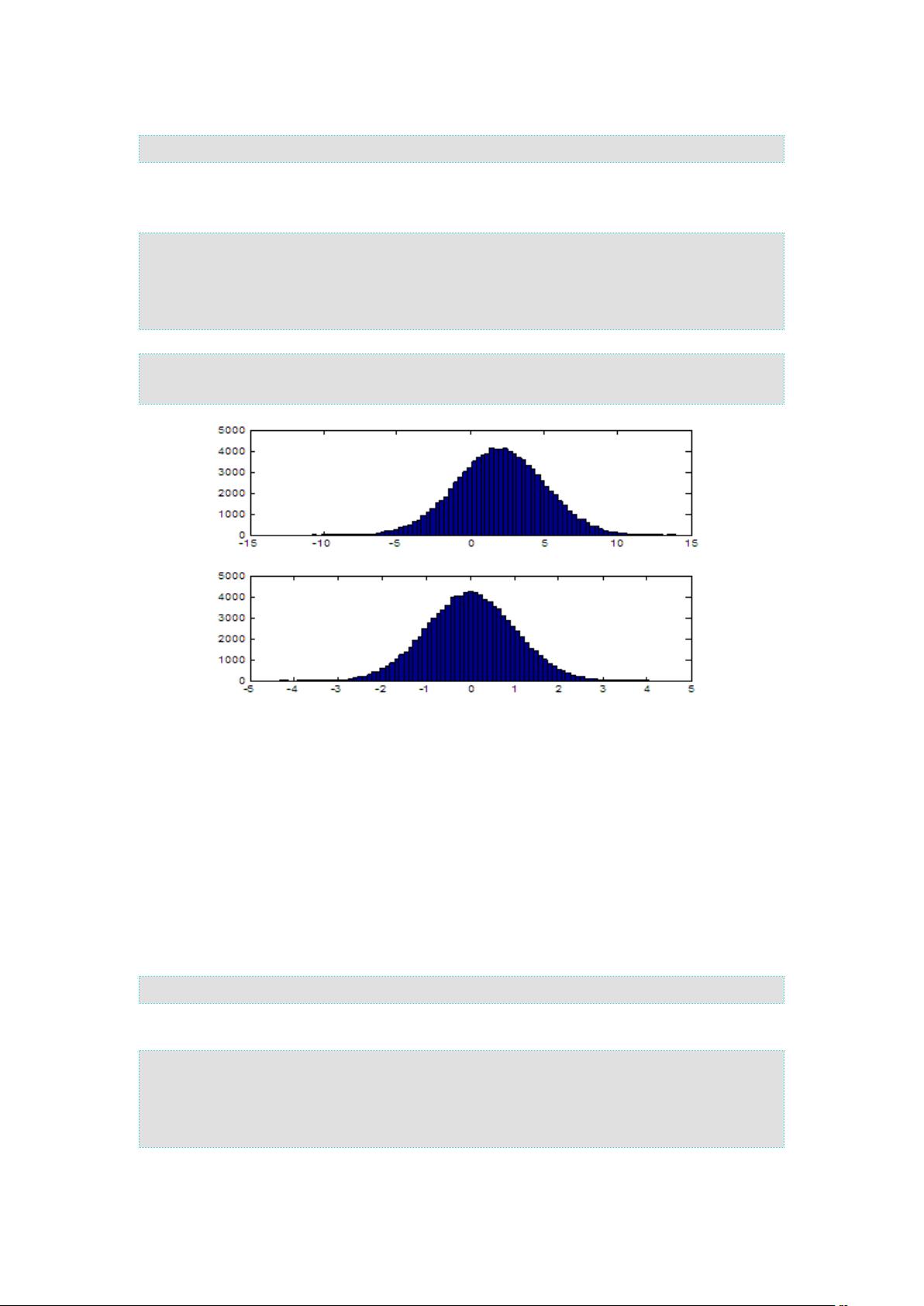 随着抽样的样本数量增加，积分的近似值会越来越接近实际值。尽管这种方法在初期可能误差较大，但其误差会随着样本数量的增加按照平方根定律衰减。 蒙特卡罗方法的优势在于其通用性和计算效率，尤其在高维度问题中，当积分的维度增加时，传统的数值积分方法的计算量会指数级增长，而蒙特卡罗方法则相对不受维度影响。然而，它的缺点是需要大量的随机抽样才能达到满意的精度，这在某些情况下可能耗费大量的计算资源。 MATLAB是实现蒙特卡罗算法的理想平台，因为它提供了丰富的数学函数库和高效的随机数生成工具，使得这种统计模拟方法变得简单易行。通过熟练掌握这一方法，可以解决许多在其他途径下难以解决的计算问题。