赫夫曼树:构建最优二叉树与带权路径长度详解
版权申诉
40 浏览量
更新于2024-07-03
收藏 2.24MB PPTX 举报
本课程讲义主要聚焦于第6章的"树和二叉树"中的一个重要主题——赫夫曼树及其应用。赫夫曼树是一种特殊的二叉树,它的核心概念是带权路径长度(Weighted Path Length,WPL),即每个节点的路径长度与其权值的乘积。赫夫曼树的特点在于,它是所有可能的二叉树中带权路径长度最短的树,因此也被称为最优二叉树。
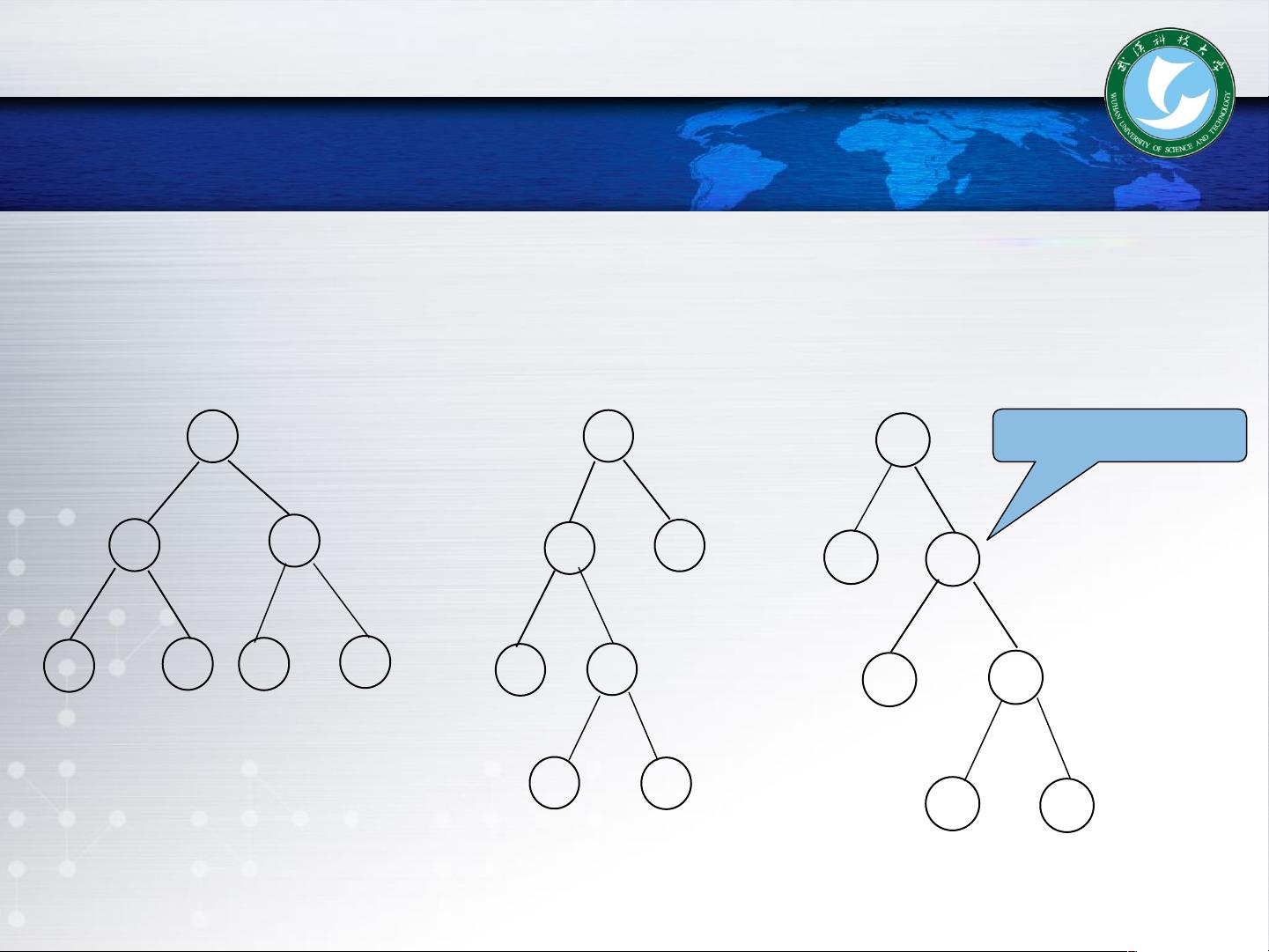
在讲解中,首先介绍了树和森林的基本概念,包括树的定义、路径以及路径长度,这是理解赫夫曼树的基础。路径是从一个节点到另一个节点经过的分支序列,而路径长度则是路径上分支的数量。树的路径长度是所有从根到叶子节点路径长度之和,而带权路径长度则是每个叶子节点的路径长度与其权值的乘积,树的带权路径长度则是所有叶子节点WPL的总和。
接下来,详细讲解了如何通过赫夫曼算法来构造这种特殊树的过程。算法步骤包括:
1. 将给定的n个权值构建n棵扩充二叉树,每棵树只有一个带有特定权值的根节点。
2. 在剩余的树集中选择权值最小的两棵树,合并它们作为新树的左右子树,新树的根节点权值为两子树之和。
3. 删除已经合并的两棵树,将新树添加回树集中,重复此过程直到只剩下一棵树,这棵剩下的树就是赫夫曼树。
赫夫曼树的一个实际应用是判定树,它在数据压缩领域有重要作用。通过对数据进行编码,使得常用字符的编码长度较短,不常用字符的编码长度较长,从而实现数据的高效存储和传输。
总结来说,这部分内容涵盖了赫夫曼树的定义、带权路径长度的概念、构造算法以及其在实际问题中的应用,对于学习数据结构和理解二叉树的优化策略具有重要意义。通过理解和掌握这些概念,学生可以深入理解如何利用赫夫曼树在信息理论和计算机科学中的优化解决方案。
126 浏览量
2022-01-06 上传
2021-10-05 上传
103 浏览量
2021-09-22 上传
2021-10-05 上传
2021-10-05 上传
2021-10-05 上传
2021-10-08 上传