布尔代数与逻辑部件：PPT讲解

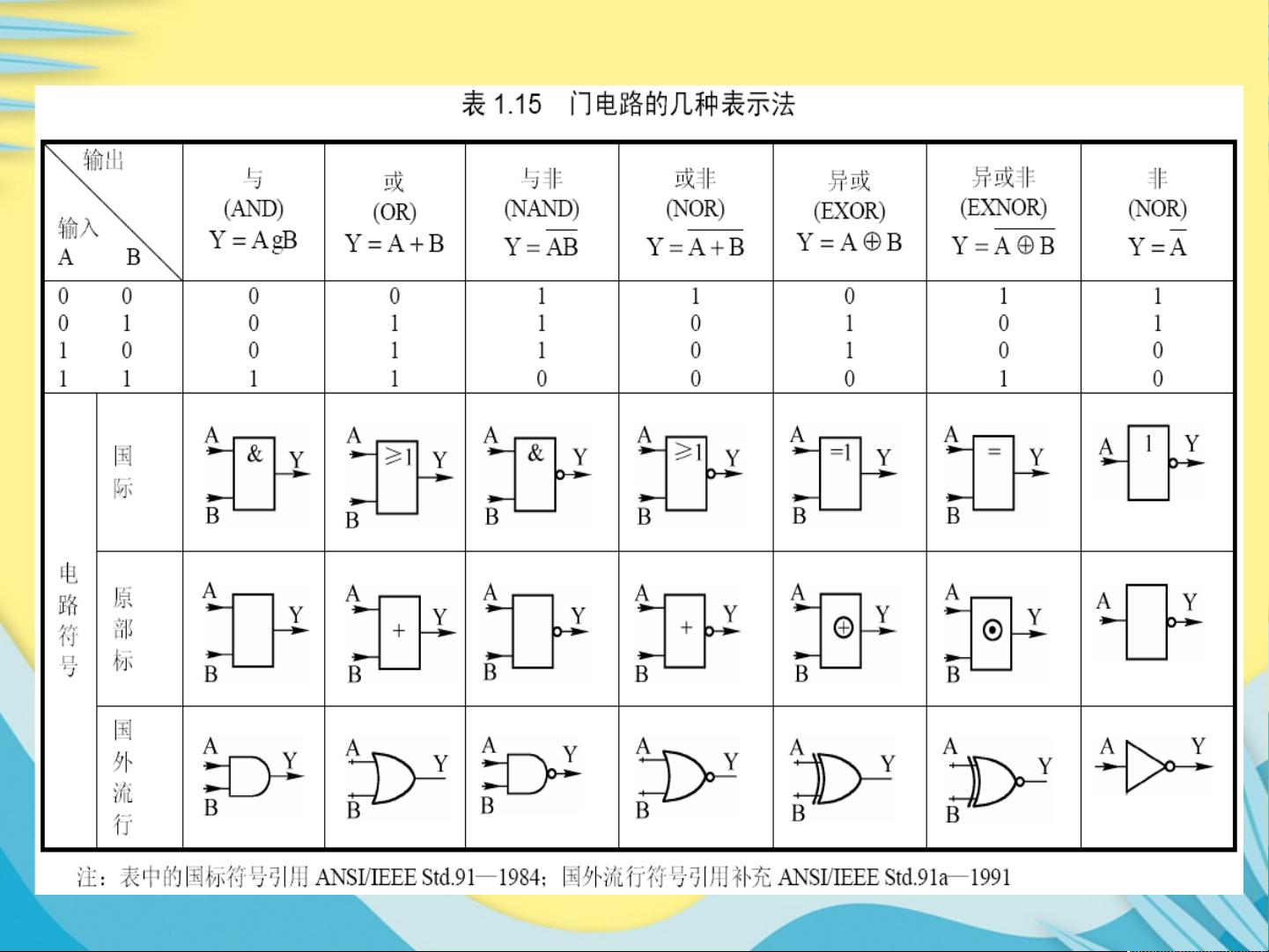
"计算机的逻辑部件修改过推选PPT文档.ppt" 布尔代数是计算机逻辑设计中的基础理论，它在数字电路设计、计算机硬件系统和逻辑编程等领域有着广泛的应用。布尔代数由乔治·布尔创立，以命题作为基本元素，并定义了三种基本逻辑操作：与（AND）、或（OR）和非（NOT）。这些操作符可以组合成更复杂的布尔函数，用于表示和分析逻辑关系。 在布尔代数中，有一些基本的定律和性质，包括： 1. 变换律：加法和乘法的操作是交换的。例如，A + B = B + A 和 A · B = B · A。 2. 结合律：加法和乘法的操作满足结合性，即无论怎样组合括号，运算结果保持不变。如 (A + B) + C = A + (B + C) 和 (A · B) · C = A · (B · C)。 3. 分配律：加法可以分配到乘法上。A + (B · C) = (A + B) · (A + C) 和 A · (B + C) = A · B + A · C。 4. 吸收律：一个项加上或乘以它自身的结果就是它本身。如 A + A · B = A 和 A · (A + B) = A。 5. 反演律：加法和乘法的互补性，A + A · B = A 和 A · B = A + B。 6. 包含律：两个项相乘再加上它们的和，结果等于原来的项。如 A · B + A · C + A = A。 7. 重叠律：重复的项在加法中可以合并。A + A = A 和 A · A = A。 8. 补充律：两个相同的项相加等于全集，相乘等于空集。A + A = 1 和 A · A = 0。 9. 0-1律：0 加任何项等于该项，1 乘任何项等于该项，而 0 乘任何项等于 0。0 + A = A, 1 · A = A, 0 · A = 0, 1 + A = 1。 布尔表达式的化简是逻辑设计的关键步骤，可以减少逻辑门的数量，提高电路的效率。化简方法包括代数化简法和卡诺图化简法。代数化简法依赖于布尔定律，但可能无法确保得到最简形式。卡诺图化简法则通过图形方式直观地简化布尔表达式，适用于变量较少的情况。每个最小项对应卡诺图上的一个方格，最小项之间的相邻性规则保证了化简的有效性。 格雷码是一种特殊的二进制编码，它的特点是任意两个相邻数值的二进制表示仅有一位不同。这种编码在数字系统中，尤其是在需要避免因位变化引起的错误时，如增量编码器和串行通信中，具有重要的应用价值。格雷码的转换可以通过特定的算法实现，也可以通过特定的逻辑电路来生成和解码。