机器学习降维方法解析：PCA原理与应用

数据的最大方差，确保在降维过程中尽可能保持数据集的变异性，从而保留关键信息。在PCA中，数据被投影到由协方差矩阵的前k个最大特征值对应特征向量组成的正交基上。这k个特征向量构成的新坐标系能够最大程度地解释原始数据的方差。 除了PCA，还有其他三种常见的降维方法： 1. 主成分分析（PCA）的非线性扩展——核主成分分析（KPCA）： PCA虽然在处理线性关系时效果良好，但对于非线性问题则显得力不从心。KPCA利用核技巧，如高斯核（RBF），将数据映射到一个高维特征空间，在这个空间中原本非线性的关系可能变得线性可分，然后再执行PCA降维。 2. 独立成分分析（ICA）： ICA的目的是找到一种映射，使得映射后的数据分量是统计独立的。这种方法假设原始数据是由一些不可观测的独立源信号混合而成的。ICA在音频信号处理和脑电图（EEG）分析等领域有广泛应用，因为它能够分离混合信号。 3. 局部线性嵌入（LLE）： LLE是一种非线性降维技术，旨在保持数据的局部结构。它假设数据点在高维空间中的邻域关系在低维空间中仍然成立。LLE通过寻找每个数据点与其最近邻居之间的线性重构权重来实现降维，确保相邻点在低维空间中仍保持相近。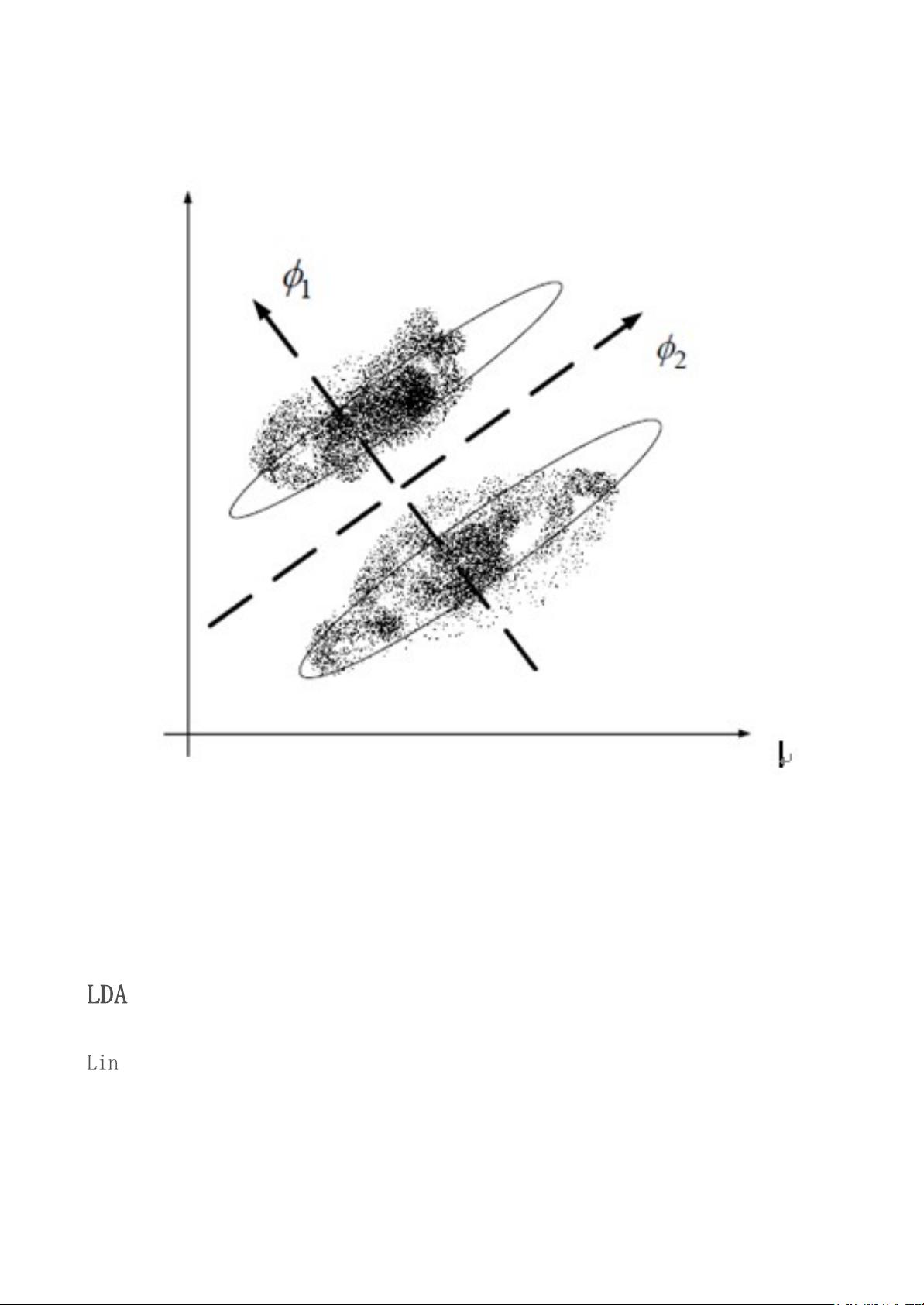 4. 线性判别分析（LDA）： LDA的主要目标是最大化类间距离，同时最小化类内距离，适用于分类任务。在降维过程中，LDA不仅考虑保持数据的方差，还考虑了类别信息，因此在分类问题上表现出色。 降维方法的选择取决于具体任务的需求。线性方法如PCA和LDA适用于线性关系明显的情况，而非线性方法如KPCA、LLE和ICA则用于处理复杂的非线性结构。在实际应用中，往往需要根据数据的特性和任务目标，结合预处理步骤和模型选择，来决定采用哪种降维技术。 降维不仅有助于减少计算复杂性，还能帮助发现数据的隐藏结构，消除冗余特征，提升模型的泛化能力。在机器学习的预处理阶段，降维通常是必不可少的步骤，它可以帮助我们更好地理解和可视化高维数据，同时也能提高后续算法的性能。因此，掌握和灵活运用这些降维方法对于任何数据科学家来说都是至关重要的。