学生指南：麦克斯韦方程详解（第一版）

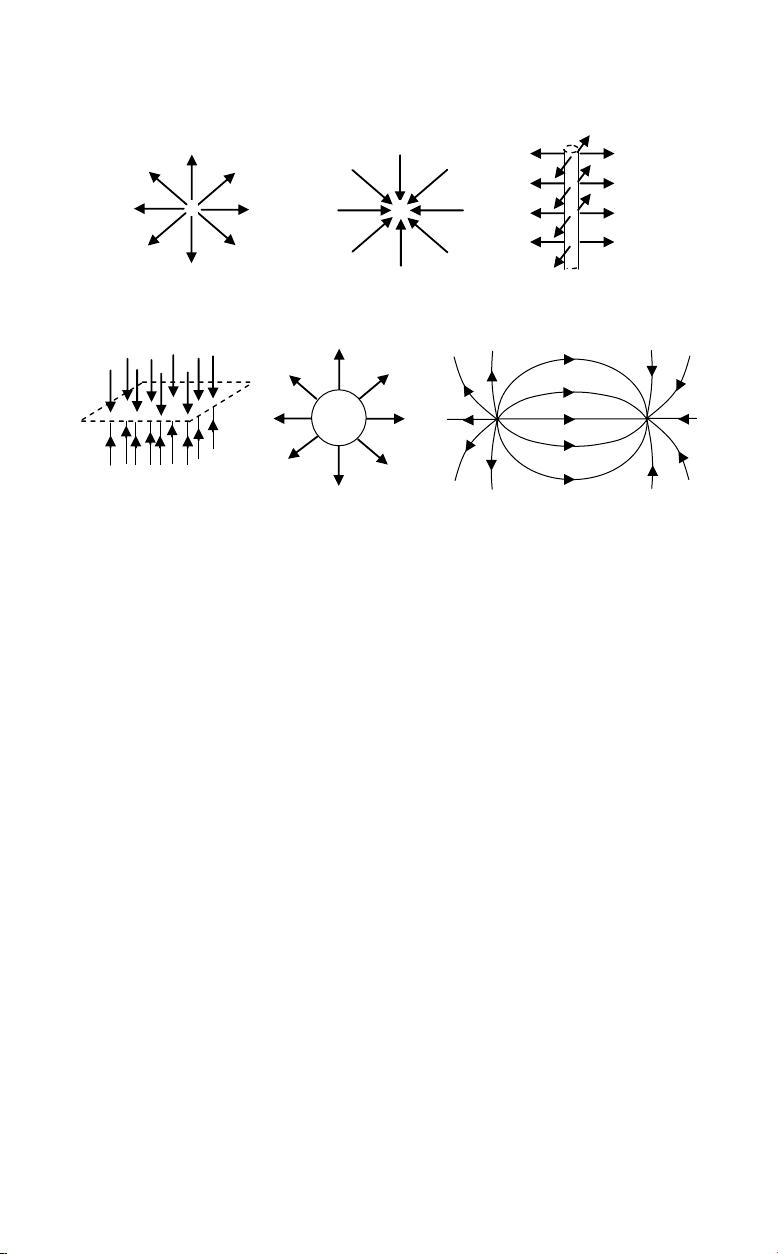
"A Student's Guide to Maxwell's Equations 1st edition" 是一本专为学生设计的权威指南，深入解析麦克斯韦方程组的核心理论。麦克斯韦方程组由四个关键公式构成：高斯电场定律、高斯磁感应定律、法拉第电磁感应定律以及安培-麦克斯韦定律。这本书将这四个方程各作为一个独立章节进行详尽探讨，作者用通俗易懂的语言阐述每个符号的物理含义，无论是积分形式还是微分形式，都力求让学生对其内在原理有深刻理解。 每一章都围绕一个方程展开，从基本概念到实际应用，帮助读者建立起电磁学的基础知识。书中的内容不仅限于理论，还通过结合，展示了如何将这些方程整合起来形成波动方程，这是电磁理论中关于光的基石。因此，这本书对于学习电磁学本科和研究生课程的学生来说是一本不可或缺的参考书籍。 此外，作者还贴心地提供了配套资源——官方网站（www.cambridge.org/9780521877619），其中包含文本中所有问题的交互式解决方案，允许学生即时查看答案或逐步得到提示。网站还提供音频 podcast，由作者亲自讲解，深入解析每个章节的重要细节和关键概念，确保学生在学习过程中能够全面理解和掌握麦克斯韦方程的精髓。 通过这本书，学生不仅能掌握麦克斯韦方程的基本理论，还能通过实践和互动式学习方式深化对电磁现象的理解，为他们在电磁学领域的研究和学习打下坚实的基础。这本书是一本实用且富有深度的学习工具，值得所有对此感兴趣的学子珍藏和探索。