递推方程与算法分析：从Fibonacci数列到Hanoi塔问题

"《算法与数据结构》—递推方程及算法分析" 本文主要探讨了在算法和数据结构领域中，递推方程的概念及其在解决问题中的应用，以Fibonacci数列和Hanoi塔问题为例进行深入解析。 首先，递推方程是一种描述序列中元素之间的关系的方式，通常用于定义序列的后续项。Fibonacci数列是一个经典的递推方程实例，它的定义是基于前两项之和来计算下一项。Fibonacci数列的递推方程为： F(n) = F(n-1) + F(n-2)，对于初始条件F(0) = 1, F(1) = 1。 这个递推方程表明，Fibonacci数列的每一项都是前两项的和。通过递推，我们可以求出数列中的任意一项，例如，F(2) = F(1) + F(0), F(3) = F(2) + F(1)，依此类推，直至找到所需项。 递推方程的解是将序列中的项表示为项号n的函数。对于Fibonacci数列，我们可以通过迭代或闭合形式（Binet's公式）来找到F(n)。这里我们展示了迭代解的简化过程，证明了递推方程的解是唯一确定的。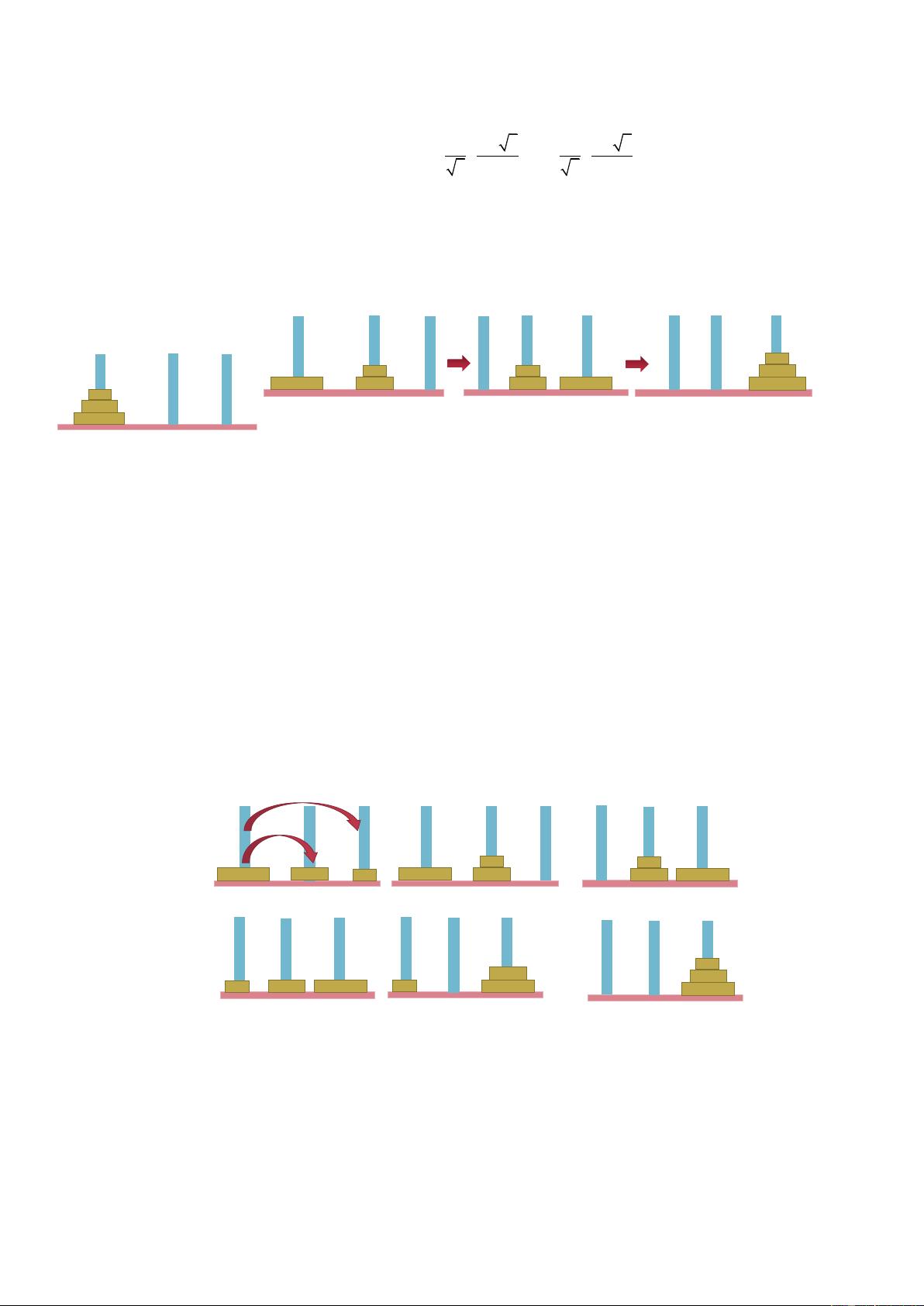 接下来，我们讨论了Hanoi塔问题，这是一个典型的递归问题。Hanoi塔包含三个柱子和n个盘子，目标是将所有盘子从柱子A移动到柱子C，每次只能移动一个盘子，并且不允许大盘子位于小盘子之上。这个问题可以通过递归策略来解决。 Hanoi塔问题的递归算法可以表示为以下伪代码： ``` Hanoi(A, C, n): if n == 1: move(A, C) // 将一个盘子直接从A移动到C else: Hanoi(A, B, n-1) // 将n-1个盘子从A移动到B move(A, C) // 将剩下的一个盘子从A移动到C Hanoi(B, C, n-1) // 将B上的n-1个盘子移动到C ``` 这个算法的时间复杂度分析表明，移动n个盘子需要进行\(2^n - 1\)次操作。递推关系如下： \(T(n) = 2 \cdot T(n-1) + 1\) 这里的\(T(n)\)表示移动n个盘子所需的步骤数，这个递推方程揭示了问题规模每增加一倍，操作次数翻倍的性质。 通过这两个例子，我们可以看到递推方程在算法设计和分析中的重要作用。递推方程不仅能够帮助我们理解和生成算法，还可以用来评估算法的效率，为实际问题提供解决方案。理解并掌握递推方程的运用，是提升算法分析能力的关键部分。