图论基础：无向图、有向图与带权图的概念

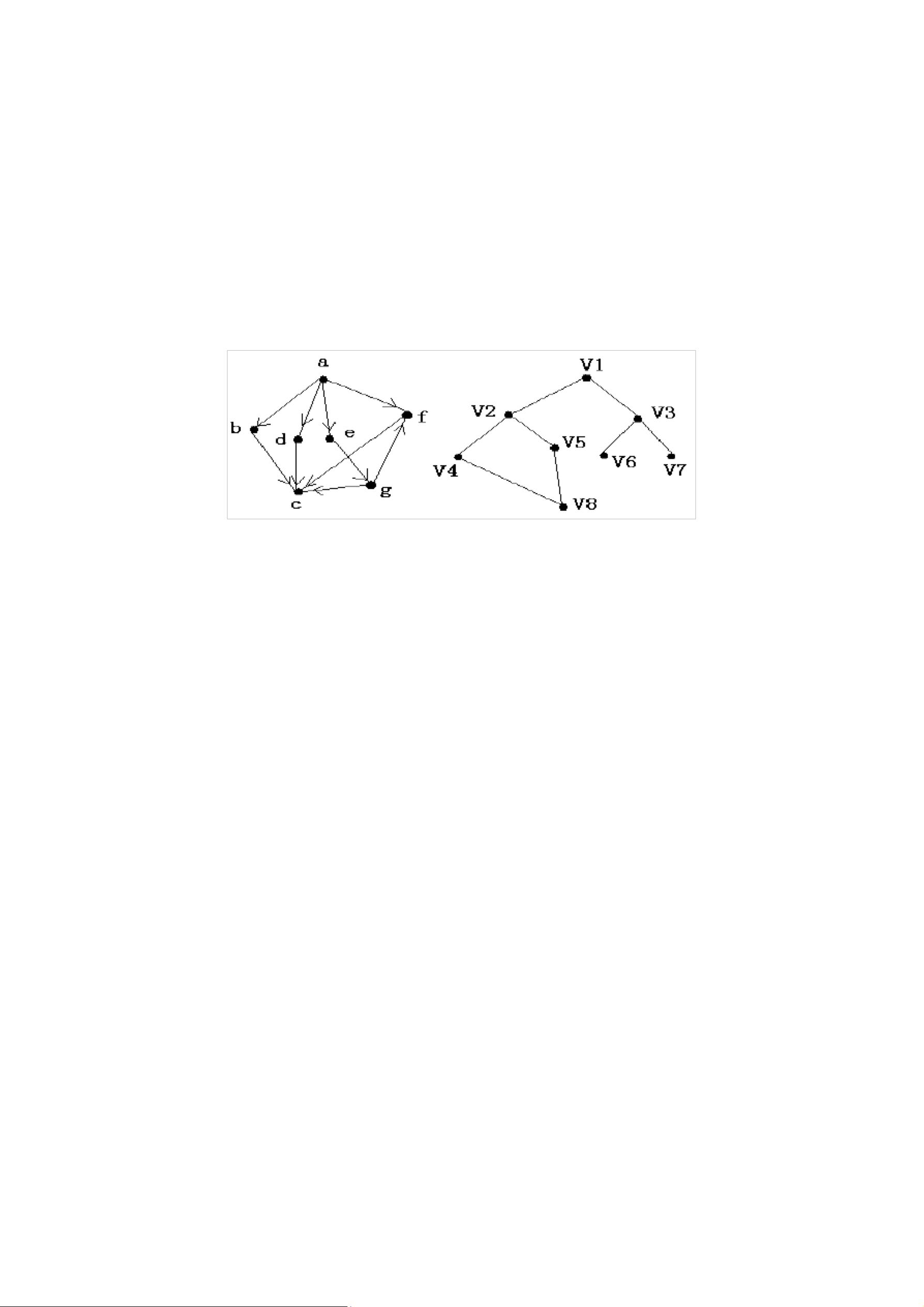
"图论中的概念及重要算法" 在计算机科学和数学中，图论是一门研究点和点之间连接关系的理论，它在很多领域都有应用，包括网络设计、算法分析、数据库结构等。以下是对图论中一些基本概念的详细解释： 1. **图的概念** 图是由顶点（或节点）和边构成的数据结构。形式上，一个图G可以表示为一个二元组G=(V,E)，其中V是非空有限集，代表顶点集合，E是边的集合。边通常用一对顶点来表示，如(v_x, v_y)，其中v_x和v_y都是V中的元素。 2. **无向图和有向图** - **无向图**：边没有方向，即边(v_x, v_y)与边(v_y, v_x)视为同一条边。例如图A和图C，它们的边用圆括号表示。 - **有向图**：边具有方向性，边表示为<v_x, v_y>，其中v_x是起点，v_y是终点。例如图B，边用尖括号表示，且<v_x, v_y>不同于<v_y, v_x>。 3. **带权图** 在带权图中，每条边都有一个与之相关的数值，这个数值称为权值，可以表示各种实际意义，如距离、成本、流量等。图C就是一个带权图，边上的数字代表权值。 4. **阶** 图的阶是指图中顶点的数量。例如，图A、图B和图C的阶分别是4、3和5。 5. **度** - **度**：在无向图中，一个顶点的度是与其相连的边的数量。在图A中，顶点v_1和v_2的度是3，是奇点；顶点v_3和v_4的度是2，是偶点。 - **入度和出度**：在有向图中，一个顶点的入度是其作为终点的边的数量，出度则是作为起点的边的数量。例如在图B中，顶点v_1的入度是0，出度是2；顶点v_2的入度是2，出度是1；顶点v_3的入度是1，出度是2。 6. **奇点和偶点** 奇点是度为奇数的顶点，偶点是度为偶数的顶点。在无向图中，奇点和偶点的数量总是相同的，因为每条边连接两个顶点，增加一个顶点的度的同时也会增加另一个顶点的度。 7. **终端顶点** 在有向图中，出度为0的顶点被称为终端顶点，意味着没有边从这些顶点出发。图B中的顶点v_1就是一个终端顶点。 8. **连通性和强连通性** - **连通图**：如果图中的任意两个顶点都通过一系列边相连，则称该图是连通的。 - **强连通图**：对于有向图，如果任意两个顶点v_x和v_y都存在从v_x到v_y的有向路径和从v_y到v_x的有向路径，则称该图是强连通的。 9. **树** 一棵树是连通的无环图，它在图论中有着特殊的地位，广泛应用于数据结构和算法中，如二叉树、AVL树、红黑树等。 10. **最短路径问题** 在带权图中，寻找两个顶点之间的最短路径是一个重要的问题，常见的算法有Dijkstra算法和Floyd-Warshall算法。 这些概念构成了图论的基础，理解和掌握它们对于解决复杂问题，特别是与网络、路径规划和优化相关的问题至关重要。在实际应用中，图论算法被广泛用于路由选择、社交网络分析、物流配送、交通网络设计等多个领域。