贝叶斯决策方法在随机模式分类中的应用

"贝叶斯决策分类器是基于统计学中的贝叶斯定理进行模式识别的一种方法。这种方法主要用于处理随机性模式的分类问题，它根据先验概率和后验概率来做出最优的决策。贝叶斯决策分类器的基础在于理解概率分布和统计规律，通过全概率公式和贝叶斯公式计算不同类别出现的概率，从而得出最佳分类规则。 在统计分类中，我们将现象或事物分为确定性和随机性两类。确定性事件在特定条件下必然发生或不发生，而随机性事件则有多种可能的结果，我们无法预测具体会发生哪一种，但可以通过概率分布来描述这些结果的统计规律。随机模式识别的核心就是贝叶斯决策，它根据不同的准则函数来制定分类规则，不同的准则会得到不同的分类结果。 贝叶斯决策理论强调利用先验概率（即在观察数据前已知的类别的概率）和条件概率（即给定特征值时属于某个类别的概率）来做出最优化的决策。全概率公式是计算一个事件发生的总概率的关键工具，通过将样本空间划分为互斥的子集（即划分），我们可以计算出事件在任何子集发生后的总体概率。贝叶斯公式则用于反向计算条件概率，即在已知观测数据的情况下，推断未知参数的概率。 在贝叶斯决策分类器中，我们通常会遇到几种重要的准则，例如最小错误率准则、最大后验概率准则和最小风险准则。最小错误率准则旨在选择错误率最低的分类，最大后验概率准则则是选择后验概率最大的类别，而最小风险准则则是在考虑误分类成本的情况下选择风险最小的分类决策。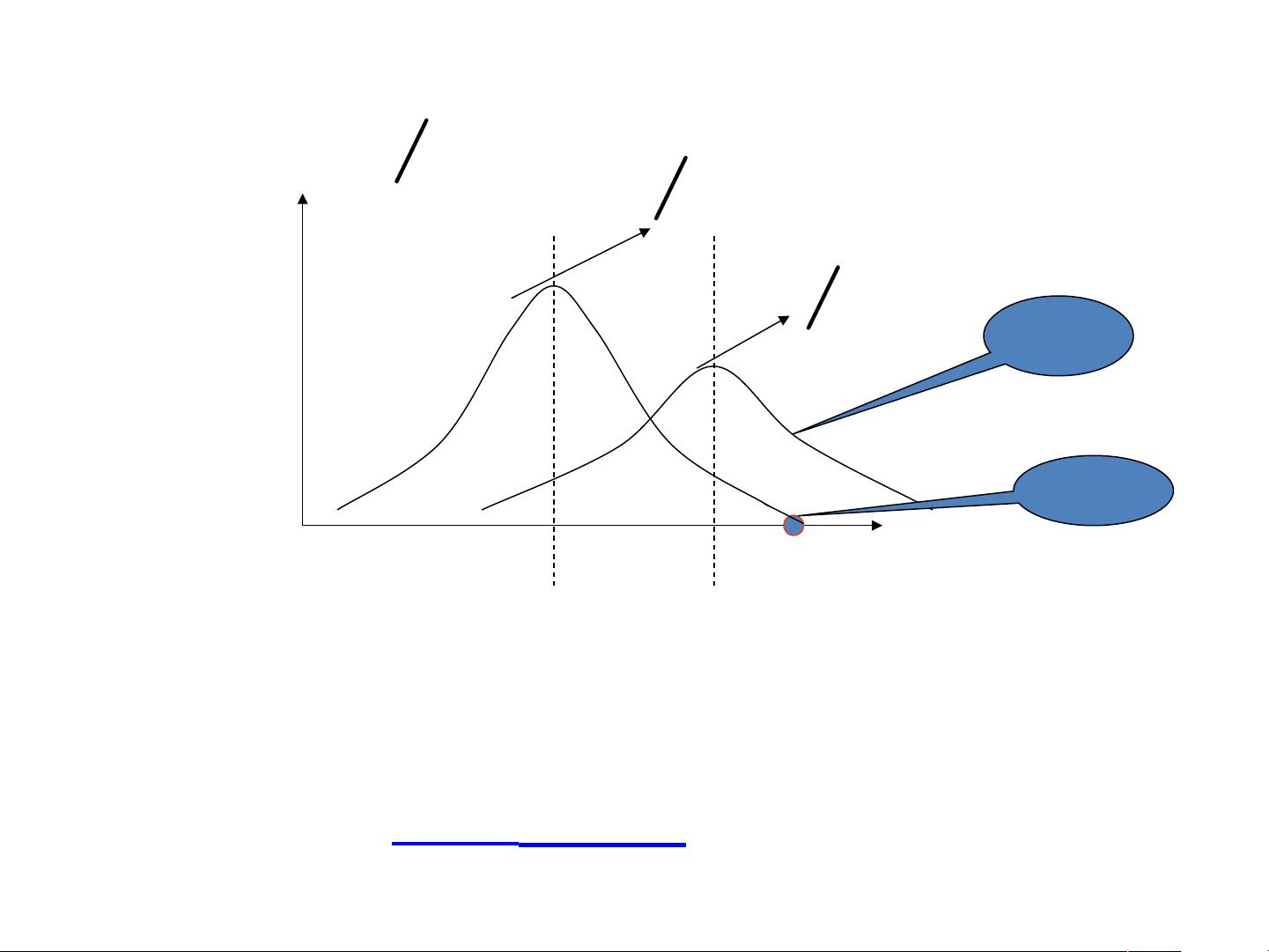 对于具有正态分布特性的模式类，我们可以使用高斯分布来建模，并计算判决函数，以决定样本应被分配到哪个类别。性能分析通常涉及计算误分类率和其他相关指标，以评估分类器的效果。 贝叶斯决策分类器是一种强大的统计工具，尤其适用于处理有噪声和不确定性的情况。通过理解和应用概率论中的基本概念，如划分、全概率公式、贝叶斯公式，我们可以构建出高效的分类系统，从而在诸如文本分类、图像识别等领域取得优秀的性能。"