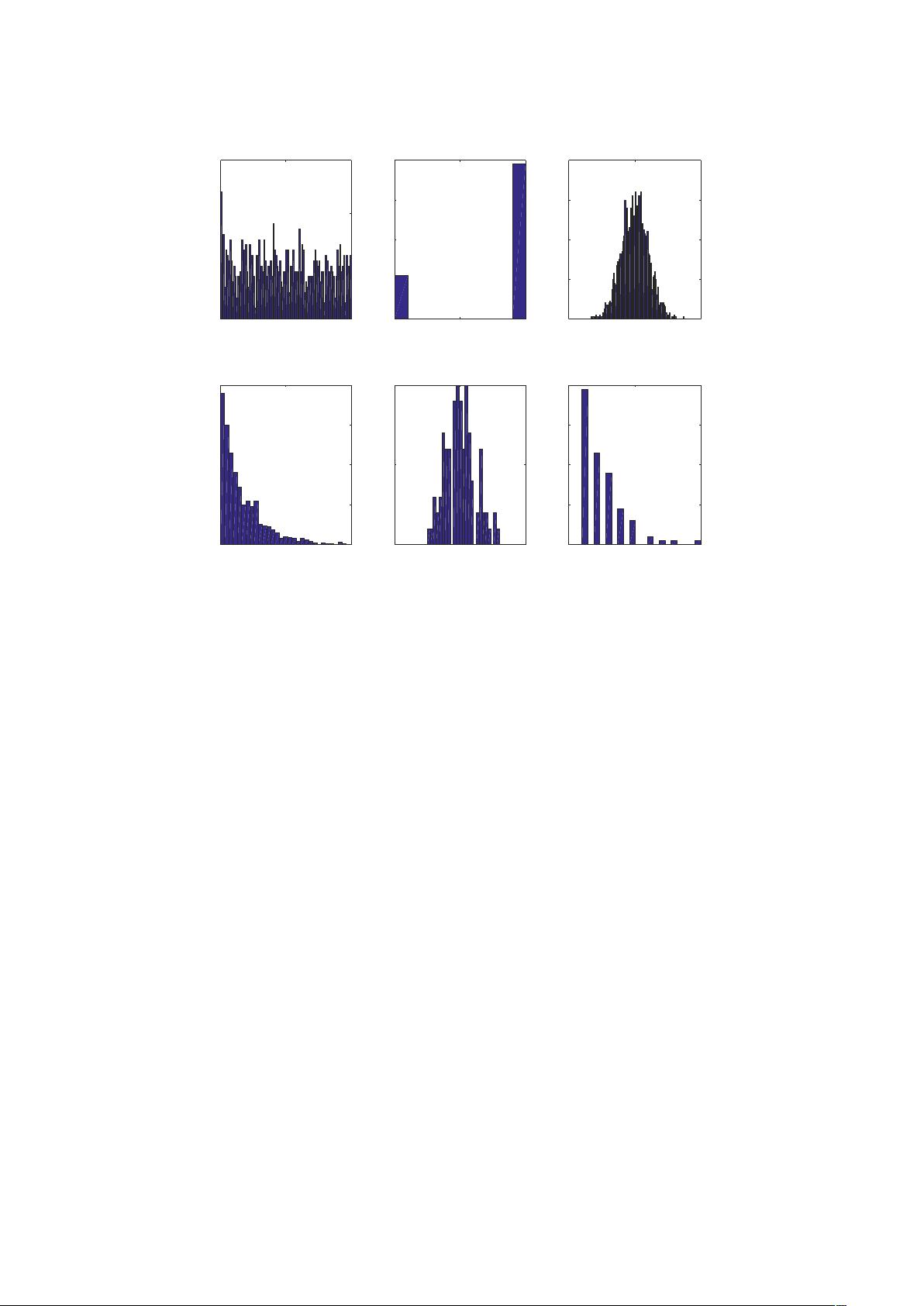
六种随机数生成方法及Matlab实现：均匀分布与伯努利分布详解

本文档深入探讨了随机数在MATLAB中的产生原理及其在六种常见概率分布（均匀分布、泊松分布、几何分布、二项分布、指数分布和正态分布）下的实现。首先，我们关注的是均匀分布，它采用同余法生成随机数序列，通过选择适当的模数M（如10^10、2*10^10或10^12）和乘法因子λ（如7、5^13或5^17），确保周期性序列具有更好的随机性。为了验证生成的随机数是否符合均匀分布，作者使用了统计检验，如通过计算均值、方差以及使用`unifit`函数估计置信区间，结果显示实验结果接近理论值。 伯努利分布部分介绍了如何基于（0,1）均匀分布的随机数来模拟这种离散概率分布。其基本思想是根据随机变量的概率P(X_i)，确定每个事件发生的概率。在MATLAB实现中，当n=2时（代表两个可能的结果），使用循环和阈值判断来生成随机变量。作者还展示了用这种方式生成的伯努利分布的直方图。 文档中提到的其他分布同样涉及相应的理论基础和MATLAB代码示例，但此处未提供详细步骤。通过这些实例，读者可以了解到如何在MATLAB中使用不同的随机数生成方法，以及如何评估生成的随机数是否符合期望的概率分布特性。这对于进行数值模拟、数据分析和统计建模等领域的工作者来说是非常实用的知识。理解这些原理和实践技巧，有助于提高在实际问题中的随机数生成质量和效率。