SPSS线性回归分析详解

"线性回归菜单简介-SPSS软件分享" 线性回归是一种广泛使用的统计方法，主要用于分析两个连续变量之间的关系。在SPSS软件中，线性回归功能可以帮助用户研究自变量如何影响因变量，并建立预测模型。描述中提到的"回归的原理"涉及到线性回归的基本概念和公式。 线性回归的核心思想是找到一条直线，这条直线能够最好地描述自变量x与因变量y之间的关系。一元线性回归方程可以表示为：y = a + bx，其中a是截距，代表当x等于0时y的预期值；b是斜率，表示x每增加一个单位，y平均改变的量。在实际应用中，这些参数是通过对观测数据进行最小二乘拟合来估计的，目的是使得所有数据点到回归线的距离平方和最小。 "线性回归的适用条件"是确保结果可靠的重要前提。这些条件包括： 1. 线性趋势：自变量和因变量之间的关系必须是线性的，即它们的关系可以用一条直线近似。 2. 独立性：每个因变量的观测值是独立的，不受其他观测值的影响。 3. 正态性：自变量的任何线性组合应服从正态分布，这通常意味着残差（观测值与预测值的差）也需服从正态分布。 4. 方差齐性：自变量的不同水平下，因变量的方差是恒定的，这意味着误差项的方差是常数。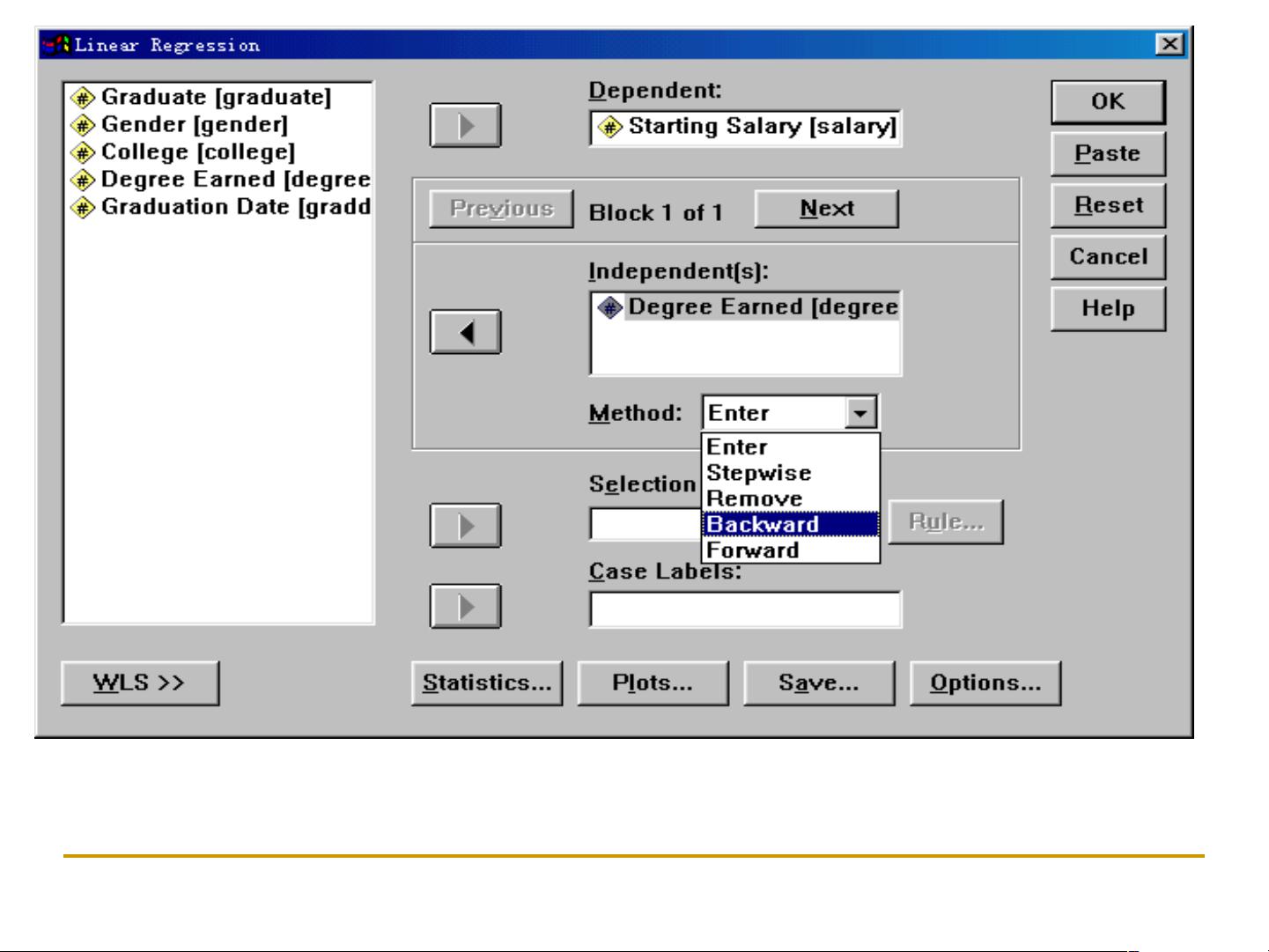 "线性回归菜单简介"部分介绍了SPSS软件中的操作。在"Linear Regression"对话框中，有两种常用的方法： 1. Enter法：默认选择，所有选定的自变量都会被纳入回归模型，不进行变量选择。 2. Stepwise法：逐步法，根据预设的标准，如显著性水平，选择对因变量贡献最大的自变量进入模型。这种方法可以帮助用户筛选出对模型影响显著的变量。 通过SPSS的线性回归功能，用户可以轻松地进行回归分析，评估自变量对因变量的影响，同时检查模型的拟合度和预测能力。此外，还可以进行假设检验，如F检验、t检验和R²值计算，以评估模型的整体效果和单个自变量的重要性。线性回归是预测和探索变量间关系的有力工具，在社会科学、经济学、医学研究等多个领域有着广泛应用。