智能汽车轨迹控制：车辆运动学与动力学模型解析

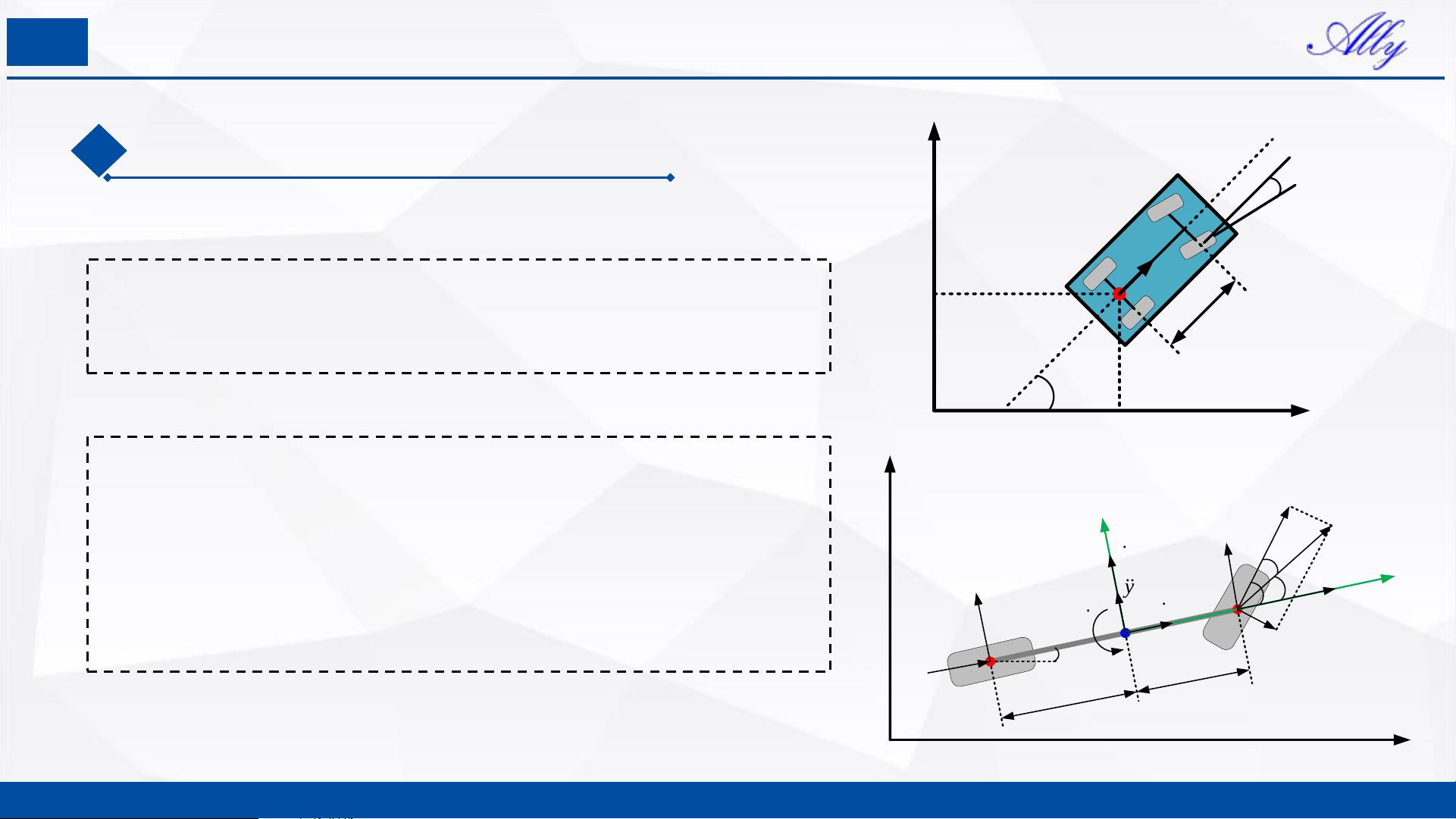
"本资源是关于智能汽车路径规划与轨迹跟踪的系列算法讲解，重点聚焦在车辆的运动学和动力学模型。课程由Ally于2021年3月1日创作，内容涵盖了轨迹跟踪控制算法。车辆运动学模型被视为刚体，只考虑位姿、速度和前轮转角等关系，而动力学模型则涉及力的影响，如轮胎侧偏。在建模时，通常通过状态空间方程来输入控制量并得到期望状态。车辆模型分为运动学模型（如自行车模型，假设二维平面运动、轮胎转速相同等）和动力学模型。车辆运动学方程描述了车辆的位置、速度和转向角之间的关系，并可以通过泰勒级数展开进行简化分析。" 在智能汽车领域，理解和建立车辆的运动模型至关重要，这关乎到路径规划和轨迹跟踪的精确性。车辆运动学模型是基础，它将车辆视为一个没有形变的刚体，主要关注车辆的位置坐标(X, Y)、航向角(θ)、速度(v)以及前轮转角(δ)。这个模型忽略了车辆内部的力作用，简化了问题，便于分析和控制。 车辆动力学模型则更复杂，它考虑了车辆与地面交互的力，如轮胎侧偏力，这对高速行驶或复杂路况下的控制尤其关键。动力学模型能够更准确地模拟车辆的实际行为，但计算和控制难度相对较大。 在构建这些模型时，常用的方法是建立状态空间方程，输入如油门、刹车或转向信号等控制量，以期望达到特定的位置、速度或角度。对于运动学模型，常采用自行车模型，这是一种简化模型，假设车辆在Z轴方向没有运动，左右轮胎转速和转向角相同，车身和悬架系统刚性，且由前轮驱动。 车辆运动学方程描述了车辆状态随时间的变化，这些方程可以用来预测车辆未来的位置和方向。例如，选取状态量为位置(X, Y)、航向角(θ)和速度(v)，控制量为前轮转角(δ)，然后根据参考轨迹的参考点(r)调整这些变量。通过泰勒级数展开，可以近似求解车辆在接近参考点时的行为，这对于轨迹跟踪控制算法的设计非常有用。 在实际应用中，这些模型和算法通常借助MATLAB等工具进行仿真和优化，以实现高效且精确的路径规划和轨迹跟踪。通过深入理解车辆的运动学和动力学特性，工程师可以设计出更智能、更安全的自动驾驶系统。