透镜的傅里叶变换性质与频率特性解析

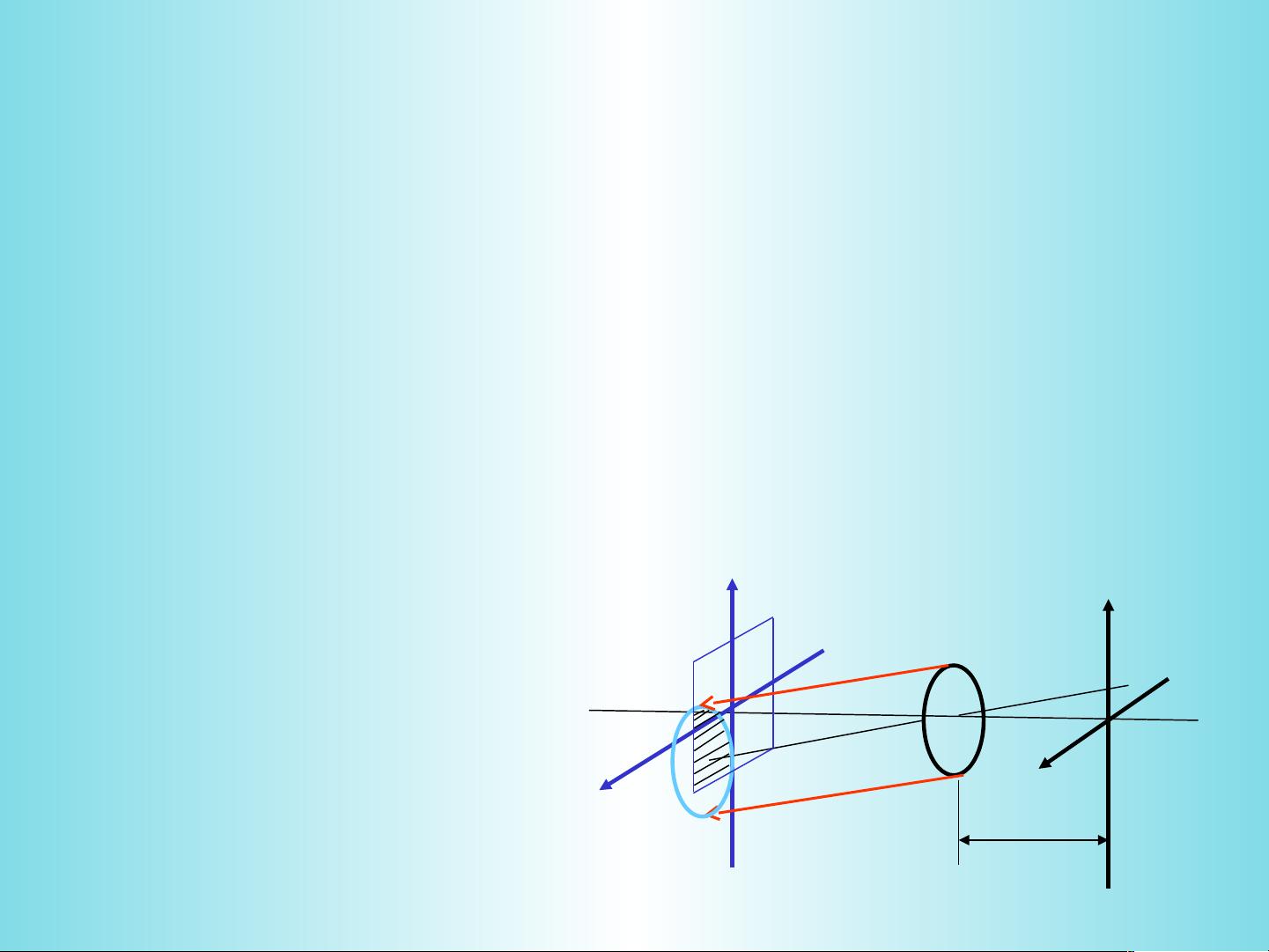
"傅里叶全息照相频率特性" 傅里叶全息照相是一种光学成像技术，它利用了傅里叶变换原理来分析和重建物体的光场信息。这种技术尤其关注图像的频率特性，即图像不同频率成分在成像过程中的变化。 在光学成像系统中，透镜扮演着重要的角色。3.1节中提到，透镜的位相变换作用是将入射光波的分布转换为出射光波的分布。透镜的这种作用可以用数学公式表示，即 \( U'_{xy} = (U_{xy})_{txy} exp(-jk \frac{x^2 + y^2}{2f}) \)，这里 \( U_{xy} \) 是入射光场，\( U'_{xy} \) 是出射光场，\( t \) 是透镜传递函数，\( k \) 是波数，\( f \) 是透镜的焦距，\( x \) 和 \( y \) 是空间坐标。这个公式表明，透镜不仅改变光场的振幅，还引入了一个与位置相关的位相因子。 3.2节探讨了透镜的傅里叶变换性质。透镜可以看作是一个自然的傅里叶变换器，将物体光场转化为其频谱分布。当物体位于透镜前某一距离（通常是焦距的两倍，即透镜前焦面上），透镜会将物面的光场转换为其傅里叶变换，即 \( F(x', y') = \mathcal{F}\{U(x, y)\} \)，其中 \( F \) 是频谱分布，\( U \) 是物面光场。这个过程可以用复指数函数的形式表达，涉及到透镜传递函数 \( C(x, y) \) 和位相因子 \( q \)。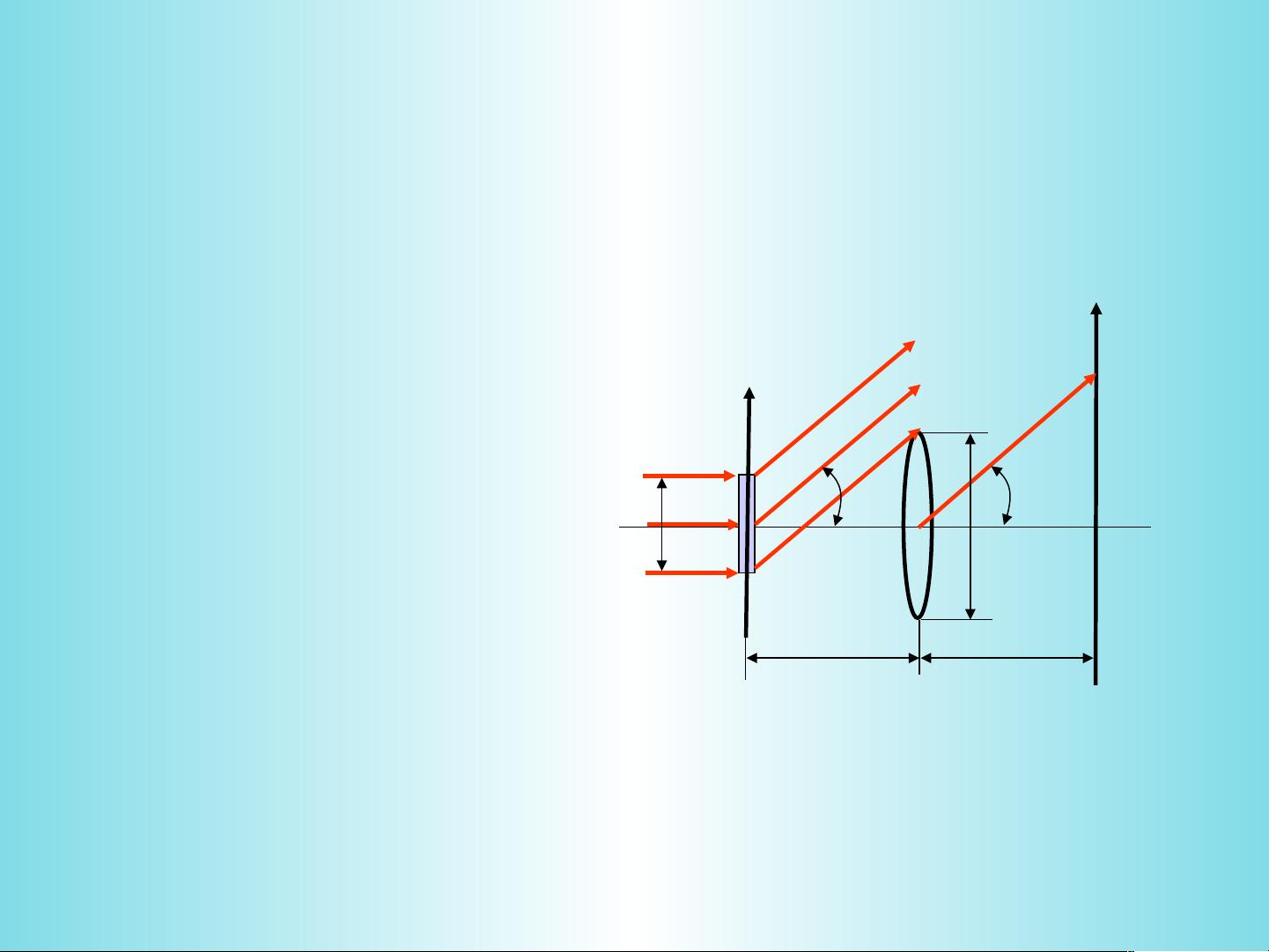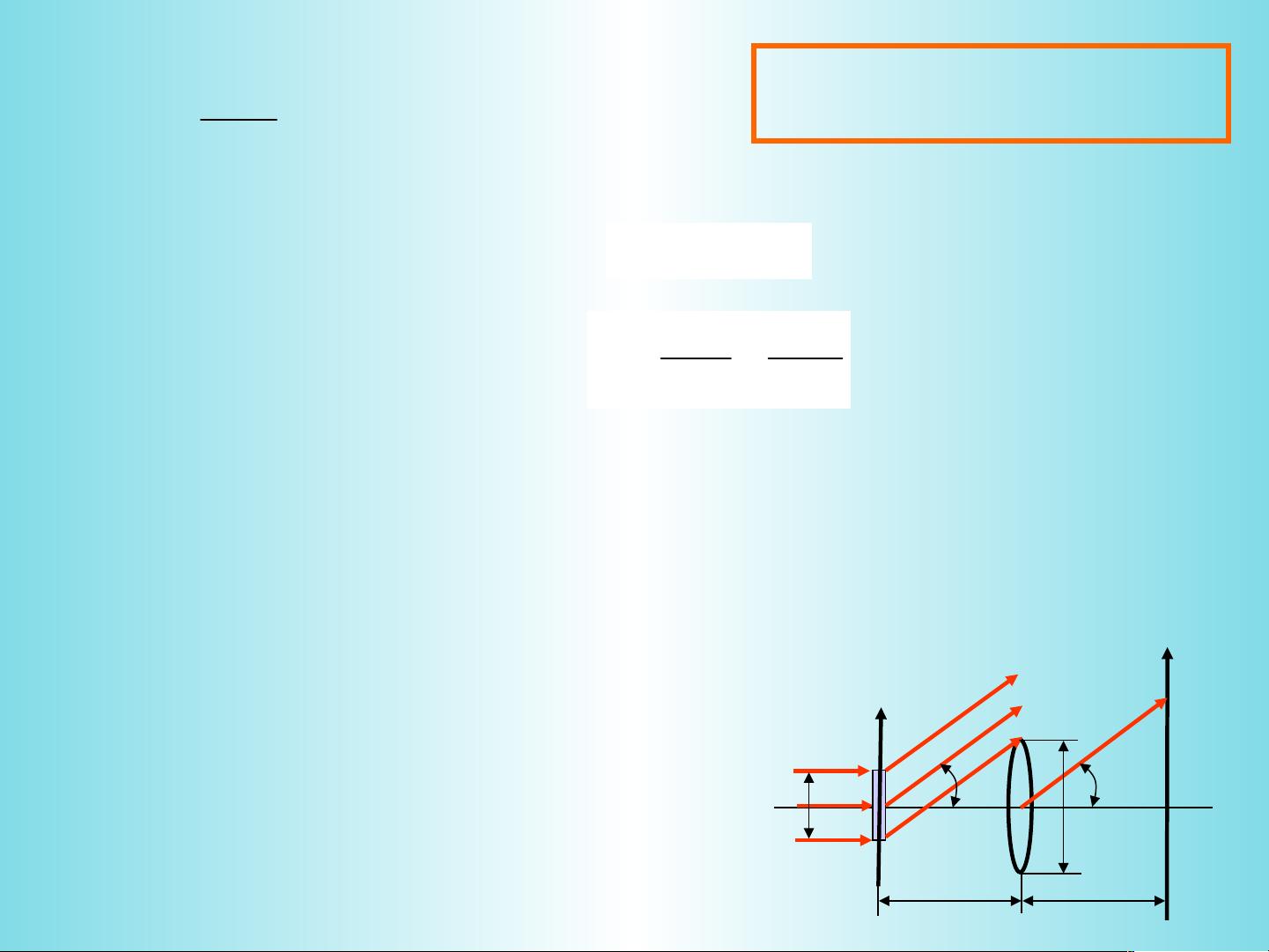 根据透镜的傅里叶变换性质，我们可以得出以下几点结论： 1. 在一般情况下，透镜后形成的频谱面上的光场分布是物频谱函数乘以一个二次位相因子的结果，这被称为准傅里叶变换，因为实际的位相变化导致了与理想傅里叶变换的差异。 2. 当物面位于透镜前焦面上时，可以得到物函数的精确傅里叶变换，这时透镜完全起到了傅里叶变换的作用。 3. 作为照明光源，可以使用单色轴向平行光或光轴上的单色点光源。然而，实践中更常见的是使用单色轴向平行光照明。 4. 物体位于透镜前焦面上，用轴向平行光照明的情况具有特殊意义，因为它能提供最理想的傅里叶变换条件。 这些理论基础对于理解和应用傅里叶全息照相技术至关重要，特别是在光学成像、信息处理、光学通信和光学数据存储等领域。通过控制光源、透镜位置和物面位置，我们可以对图像的频率特性进行分析和操纵，从而实现各种高级成像技术。