进制转换详解：十进制、二进制与十六进制的关系

"各种进制关系(60页).pdf" 在计算机科学中，理解不同进制之间的转换至关重要，特别是对于编程和数据处理。本资源详细介绍了十进制、二进制和十六进制之间的相互转换关系，这对于学习CSP-J、CSP-S以及准备NOIP等竞赛的计算机科学学生来说是基础内容。 首先，我们要知道十进制是最常见的计数系统，我们日常生活中的数字都是基于十进制的。二进制则是计算机科学的基础，所有计算机内部的运算都是基于二进制进行的，即只有0和1两个数字。十六进制则是二进制的一种便捷表示方式，它由0-9和A-F这16个符号组成，每个十六进制数字对应4位二进制数。 在转换中，我们可以使用按权展开的方式来计算。例如，二进制数10100101B可以转换为十进制，即128+0+32+0+0+4+0+1=165。同样，十进制数53转换为二进制，可以通过不断除以2取余数，然后倒序排列得到1101011B。对于小数部分，可以使用乘2取整的方法，如0.6875转换为二进制，就是不断乘2取整，得到0.10110000000000B。 对于八进制和十六进制，它们都是二进制的便捷表示。八进制每三位二进制对应一个八进制数字，而十六进制每四位二进制对应一个十六进制数字。例如，二进制数11010111B可以转换为八进制数为263O，再进一步转换为十六进制数为D7H。同样，十进制数165转换为十六进制，先转换为二进制10100101B，然后再分组得到A5H。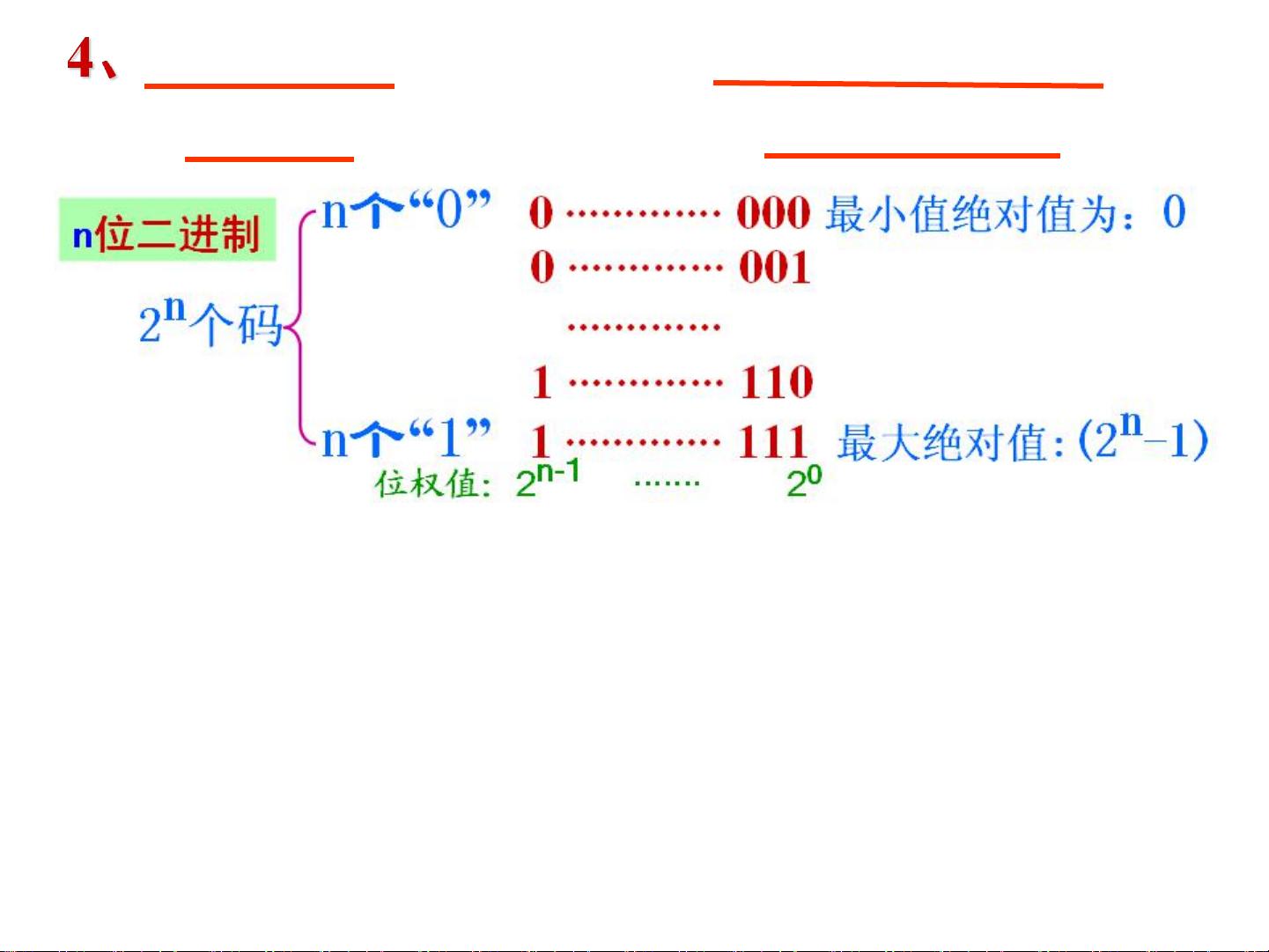 在进行进制转换时，需要记住各个位的位权值，例如在二进制中，位权值是2的幂次，从右到左依次是2^0, 2^1, 2^2, ...。同样，在八进制中是8的幂次，十六进制中是16的幂次。 理解这些转换规则对于理解和编写计算机程序非常重要，尤其是在处理二进制数据、内存地址或者进行位操作时。同时，对于参加信息学竞赛的学生来说，掌握这些基本的进制转换技巧也是必备技能，能够帮助他们解决复杂的算法问题。因此，深入理解和熟练应用各种进制之间的转换关系是计算机科学学习者的基础功底。