where yðtÞ represents the structured output associated to t.
T
out
canbecomputedbyresortingtoanode-wise output function g:
g :
R
N
R
-
R
N
Y
yðnÞ¼gðxðnÞÞ ð8Þ
where yðnÞA
R
N
Y
is the (unstructured) output associated to node n.In
this case yðtÞ is computed by applying function g to every node of t.
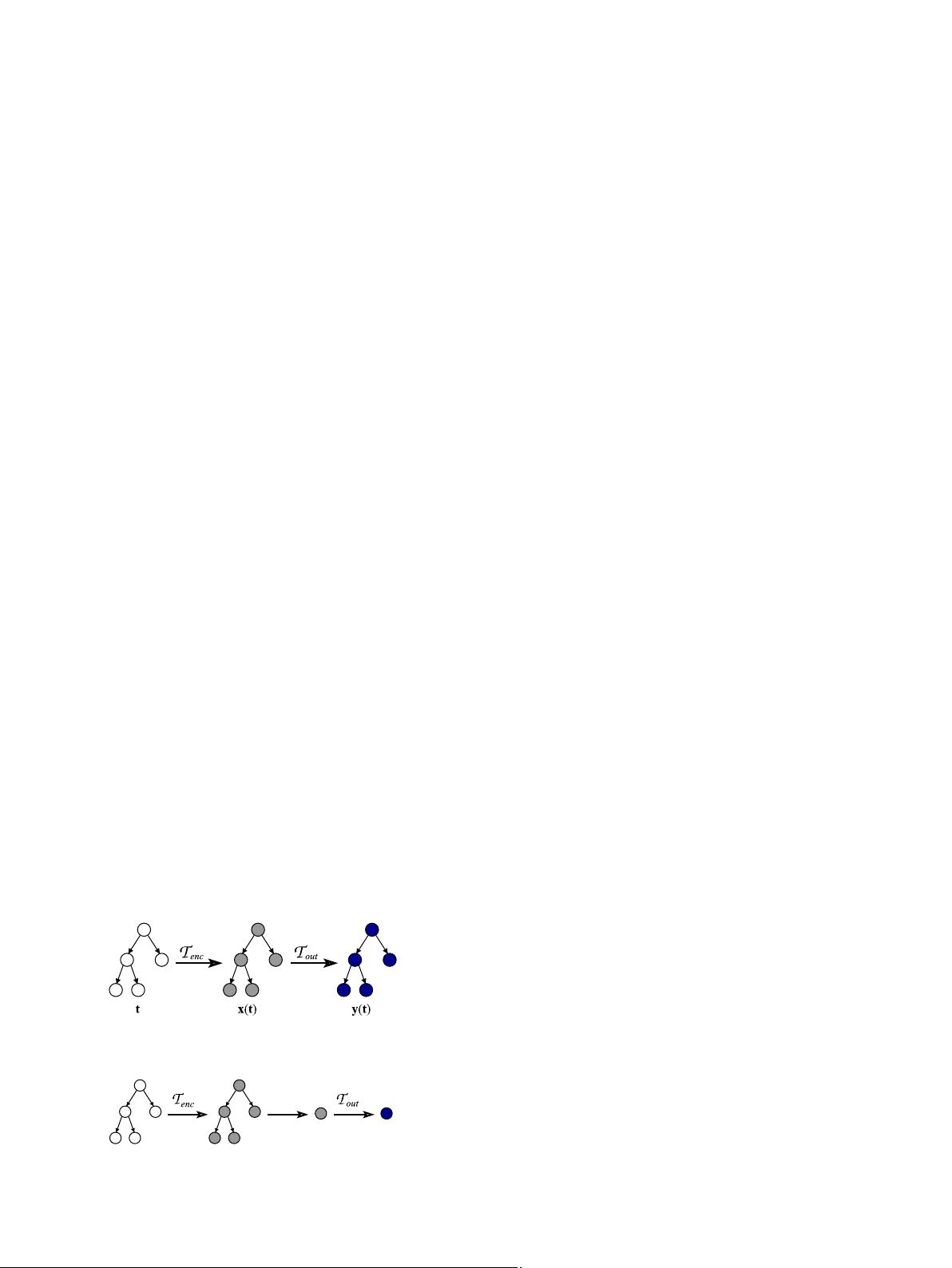
Fig. 2 summarizes the computation of t ree-to-tree structural
transductions.
For tree-to-element transductions, a state mapping function
w
is
preliminarily applied to the structured state computed by T
enc
,in
order to obtain a single fixed-size feature state, representative of
the whole input structure:
w
: ð
R
N
R
Þ
#k
-
R
N
R
ð9Þ
The unstructured fixed-size output is then computed by applying
the node-wise output function g of Eq. (8) only to the output of
the state mapping function:
yðtÞ¼gð
w
ðxðtÞÞÞ ð10Þ
In this case, yðtÞA
R
N
Y
denotes the unstructured output associated
to t. Moreover, input and output domains of T
out
of Eq. (7)
actually degenerate into the unstructured vectorial spaces
R
N
R
and
R
N
Y
respectively, and the computation of the whole transduc-
tion can be expressed as the composition of the encoding
transduction, the state mapping function and the output trans-
duction:
T ¼ T
out
JwJ
T
enc
ð11Þ
Fig. 3 graphically shows the steps of the computation of a tree-to-
element structural transduction.
Considering a supervised learning paradigm, a training set of
input trees with maximum degree k is represented by T ¼
fðt, y
target
ðtÞÞ : A ð
R
N
U
Þ
#k
, y
target
ðtÞA ð
R
N
Y
Þ
#k
g, where y
target
ðtÞ is the
target output associated to tree t in the general case of a tree
structured output (tree-to-tree transduction). In the following of
the paper, we focus on tree-to-element transductions which allow
us an immediate assessing of the TreeESN (provided with differ-
ent state mapping functions) on known problems modeling a
variety of interesting tasks on tree domains, such are classifica-
tions of trees. For the specific case of regression tasks related to
tree-to-element transductions, y
target
ðtÞ is a fixed size vector in
R
N
Y
. In the case of classification tasks with M target classes,
y
target
ðtÞ is an M-dimensional binary vector in which, for the
instances used in the experiments, the element corresponding
to the correct classification is equal to 1 and all the other
elements are equal to 0.
2.3. RecNNs and related models for processing structural
transductions
When the node-wise encoding and output functions of a
structural transduction, i.e.
t
and g in the above definitions
(Eqs. (5) and (8), respectively) are computed by neural networks,
we get RecNN models [21,7]. In the simplest architectural setting,
a RecNN consists of a recursive hidden layer, which is responsible
for the computation of
t
, and a feed-forward output layer, which
is responsible for the computation of g. Structural transductions
computed by RecNNs are usually characterized by causality,
stationarity and adaptivity, as the parameters of both the hidden
and the output layers are trained from examples. RecNNs
have been successfully applied to several real-world applica-
tive domains of relevant interest, including cheminformatics
(e.g. [25,45,29]), natural language processing [26,28] and image
analysis [24,27]. In addition, a number of results concerning
the computational capabilities of RecNN models have been
established, including universal approximation theorems for tree
domains processing [23,22]. The recursive dynamics can also be
exploited for unsupervised learning, as introduced in [46] using
self-organizing maps, or more in general in [42,43]. A recent
RecNNs variant is represented by the RelNN model [30,31], in
which encoding is based on a sequential processing of the
children of each node. The GNN model [32], based on a trained
encoding process under contractive constraints, extends the
recursive approaches allowing cyclic dynamics in the definition
of the state to process graph structures (and hence also tree
structures).
However, training RecNNs can face similar problems to those
encountered with RNNs [14,33,34], such as high computational
training costs, local minima, slow convergence and vanishing of
the gradients [47]. In particular, training RecNNs can be even
more computationally expensive than training RNNs. In this
regard, the RC paradigm represents a natural candidate for
investigating efficient approaches to RecNN modeling. Section 3
describes the TreeESN model, a first extension of the RC paradigm
to structured domains processing.
3. TreeESN model
TreeESNs are RecNNs implementing causal, stationary and
partially adaptive transductions on tree structured domains.
A TreeESN is composed of an untrained hidden layer of recursive
non-linear units (a generalized reservoir) and of a trained output
layer of feed-forward linear units (the readout). The reservoir
implements a fixed encoding transduction, whereas the readout
implements an adaptive output transduction. For tree-to-element
transductions, a state mapping function is used to obtain a single
fixed-size feature representation. The following sub-sections
describe the components of a TreeESN model.
3.1. Reservoir of TreeESN
The reservoir consists of N
R
recursive (typically) non-linear
units, which are responsible for computing the encoding of a tree
transduction by implementing the node-wise encoding function
t
of Eq. (5), which takes the role of a recursive state transition
function. Accordingly, the state corresponding to node n of a tree t
is computed as follows:
xðnÞ¼f W
in
uðnÞþ
X
k
i ¼ 1
^
Wxðch
i
ðnÞÞ
!
ð12Þ
where W
in
A
R
N
R
N
U
is the input-to-reservoir weight matrix
(which might also contain a bias term),
^
W A
R
N
R
N
R
is the
Fig. 2. Computation of a tree-to-tree structural transduction T .
x(t) y(t)
t
χ
χ(x(t))
Fig. 3. Computation of a tree-to-element structural transduction T .
C. Gallicchio, A. Micheli / Neurocomputing 101 (2013) 319–337322









