线性定常系统Lyapunov稳定性分析与定理
版权申诉
125 浏览量
更新于2024-07-07
收藏 967KB DOC 举报
"现代控制理论基础(二).doc"
现代控制理论是自动化、电子工程等领域中的核心理论,它涉及到如何稳定和优化动态系统的行为。本文主要关注的是线性定常系统的Lyapunov稳定性分析,这是现代控制理论中一个至关重要的概念。
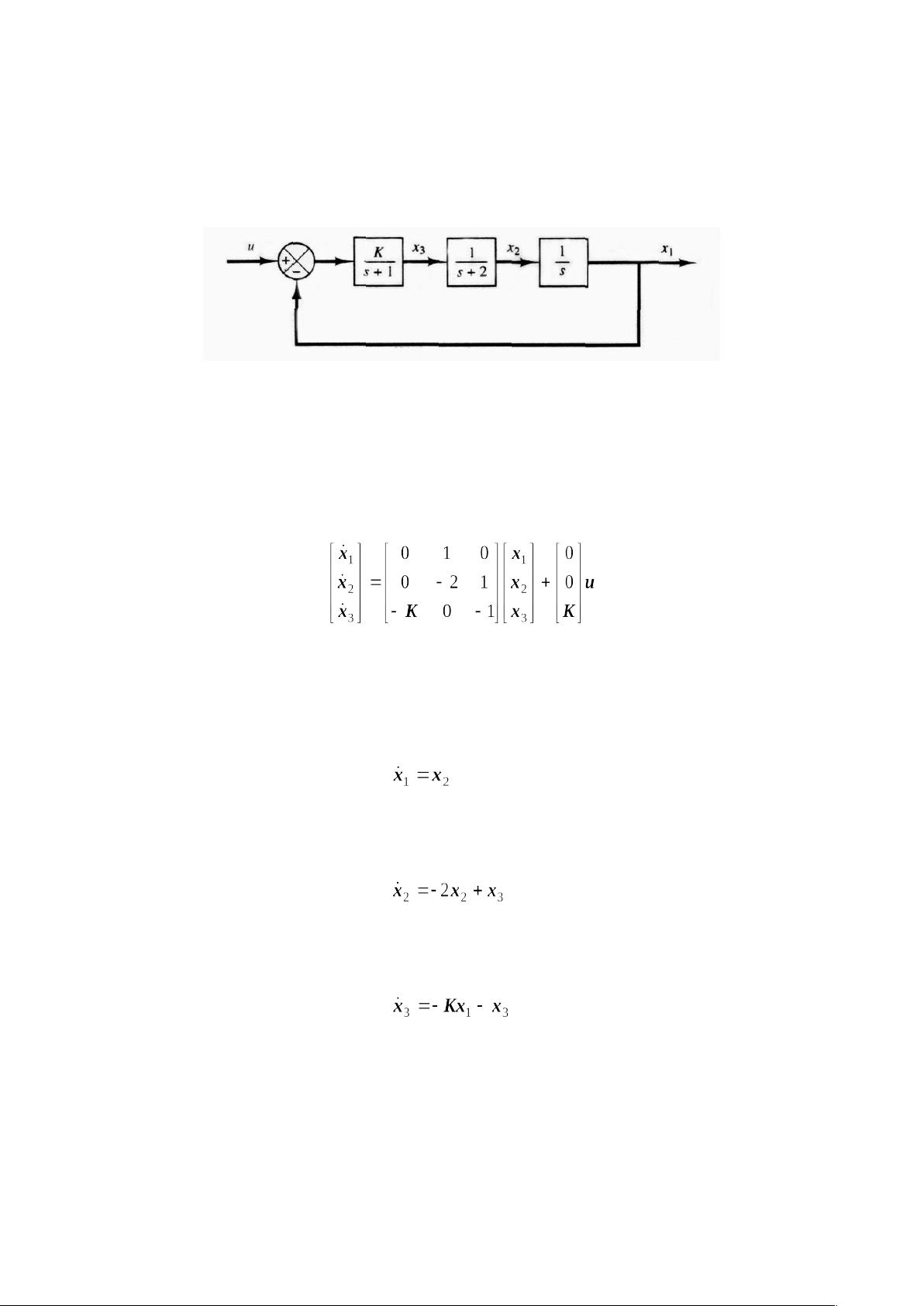
线性定常系统是指那些状态方程不随时间变化且线性的系统。给定的线性定常自治系统可以表示为[pic](4.3),其中[pic]是状态向量,[pic]是系统矩阵。如果矩阵A非奇异,即它是可逆的,系统有一个唯一的平衡状态[pic]。
Lyapunov稳定性分析是一种广泛用于研究系统稳定性的方法,它通过定义一个Lyapunov函数来判断系统的稳定性。在这里,选择了一个二次型的Lyapunov函数,即[pic],其中P是正定的Hermite矩阵。正定矩阵意味着所有特征值都是正的,这对于分析稳定性至关重要。
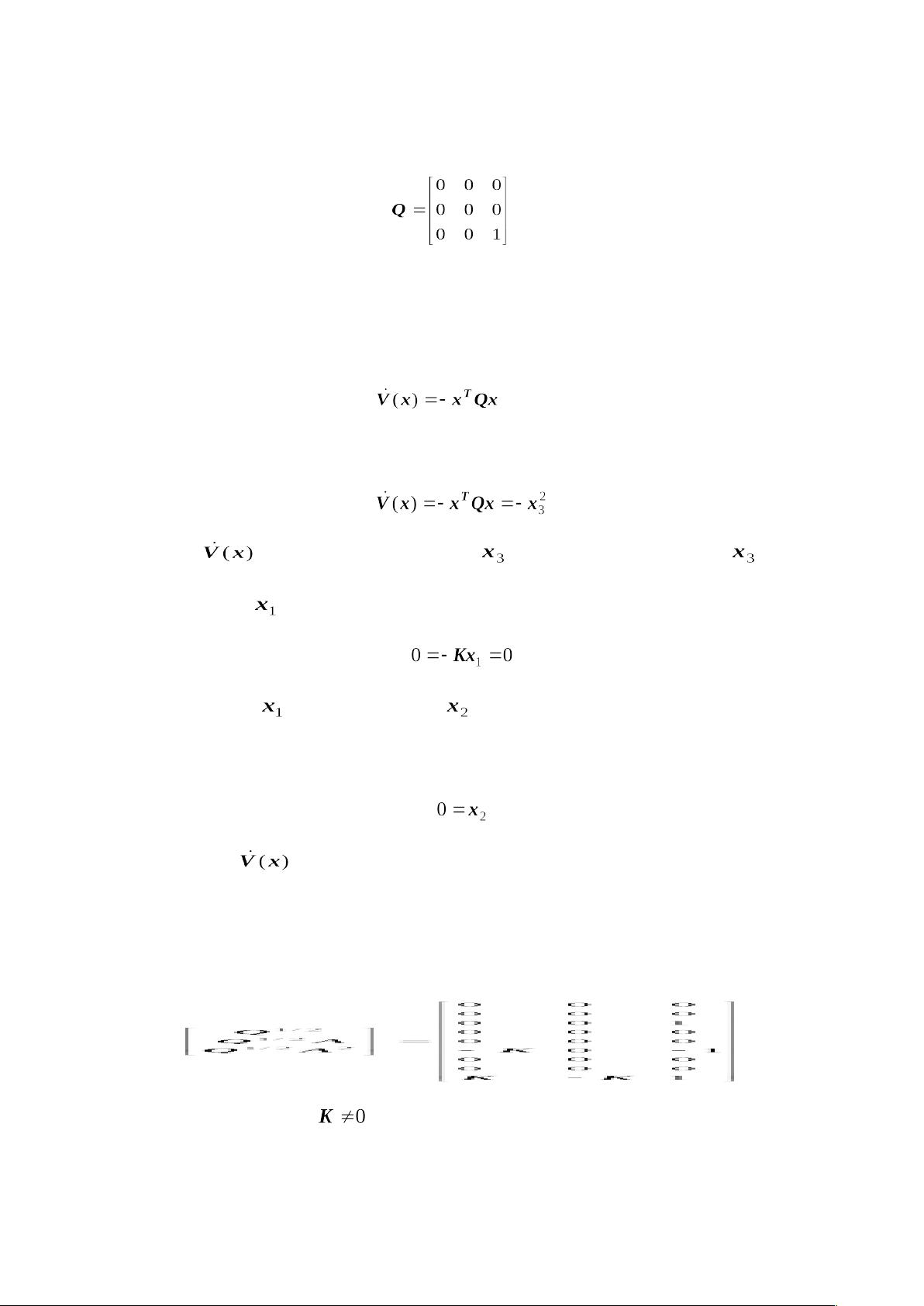
Lyapunov函数沿着系统轨迹的时间导数[pic]需满足某些条件以确保稳定性。若要系统渐近稳定,即系统状态随着时间趋向于平衡点[pic],那么[pic]应为负定矩阵。这导致了Lyapunov方程[pic]的出现,其中Q也需要是正定矩阵。
定理4.8指出,线性定常系统[pic]在平衡点[pic]渐近稳定的充要条件是存在满足Lyapunov方程[pic]的正定矩阵P和Q。这里的P和Q可以是Hermite矩阵或实对称矩阵。
解释定理4.8的几个关键点:
1. 当系统状态向量和系统矩阵都是实数时,Lyapunov函数可简化为[pic],相应的Lyapunov方程为[pic]。
2. 如果[pic]沿任何轨迹不恒等于零,Q可以取正半定矩阵。
3. 对于渐近稳定性,当使用任意正定矩阵Q或在[pic]不恒等于零时使用正半定矩阵Q,解Lyapunov方程[pic]得到的P需为正定。
4. 正定矩阵Q的选择不影响最终的稳定性判断,只要满足正定性(或正半定性,视情况而定)。
5. 确定矩阵P的元素可以通过让[pic]与矩阵-Q的元素对应相等来实现。
此外,如果正半定矩阵Q满足特定的秩条件[pic],则[pic]沿任意轨迹不恒等于零,这对分析稳定性有重要意义。
Lyapunov稳定性分析提供了一种通用的工具来分析线性定常系统的稳定性,而定理4.8提供了一个具体的计算框架来确定系统是否渐近稳定。在实际应用中,工程师通常会根据系统特性选择合适的Lyapunov函数和正定矩阵Q来进行稳定性分析。
2021-05-20 上传
2021-09-28 上传
2021-10-11 上传
2021-10-08 上传
2021-10-10 上传
2022-05-12 上传
2021-10-11 上传
2021-09-19 上传
2021-10-12 上传
成长之路514
- 粉丝: 2621
- 资源: 3万+
最新资源
- Angular实现MarcHayek简历展示应用教程
- Crossbow Spot最新更新 - 获取Chrome扩展新闻
- 量子管道网络优化与Python实现
- Debian系统中APT缓存维护工具的使用方法与实践
- Python模块AccessControl的Windows64位安装文件介绍
- 掌握最新*** Fisher资讯,使用Google Chrome扩展
- Ember应用程序开发流程与环境配置指南
- EZPCOpenSDK_v5.1.2_build***版本更新详情
- Postcode-Finder:利用JavaScript和Google Geocode API实现
- AWS商业交易监控器:航线行为分析与营销策略制定
- AccessControl-4.0b6压缩包详细使用教程
- Python编程实践与技巧汇总
- 使用Sikuli和Python打造颜色求解器项目
- .Net基础视频教程:掌握GDI绘图技术
- 深入理解数据结构与JavaScript实践项目
- 双子座在线裁判系统:提高编程竞赛效率