遗传算法应用：MATLAB实现一元函数优化

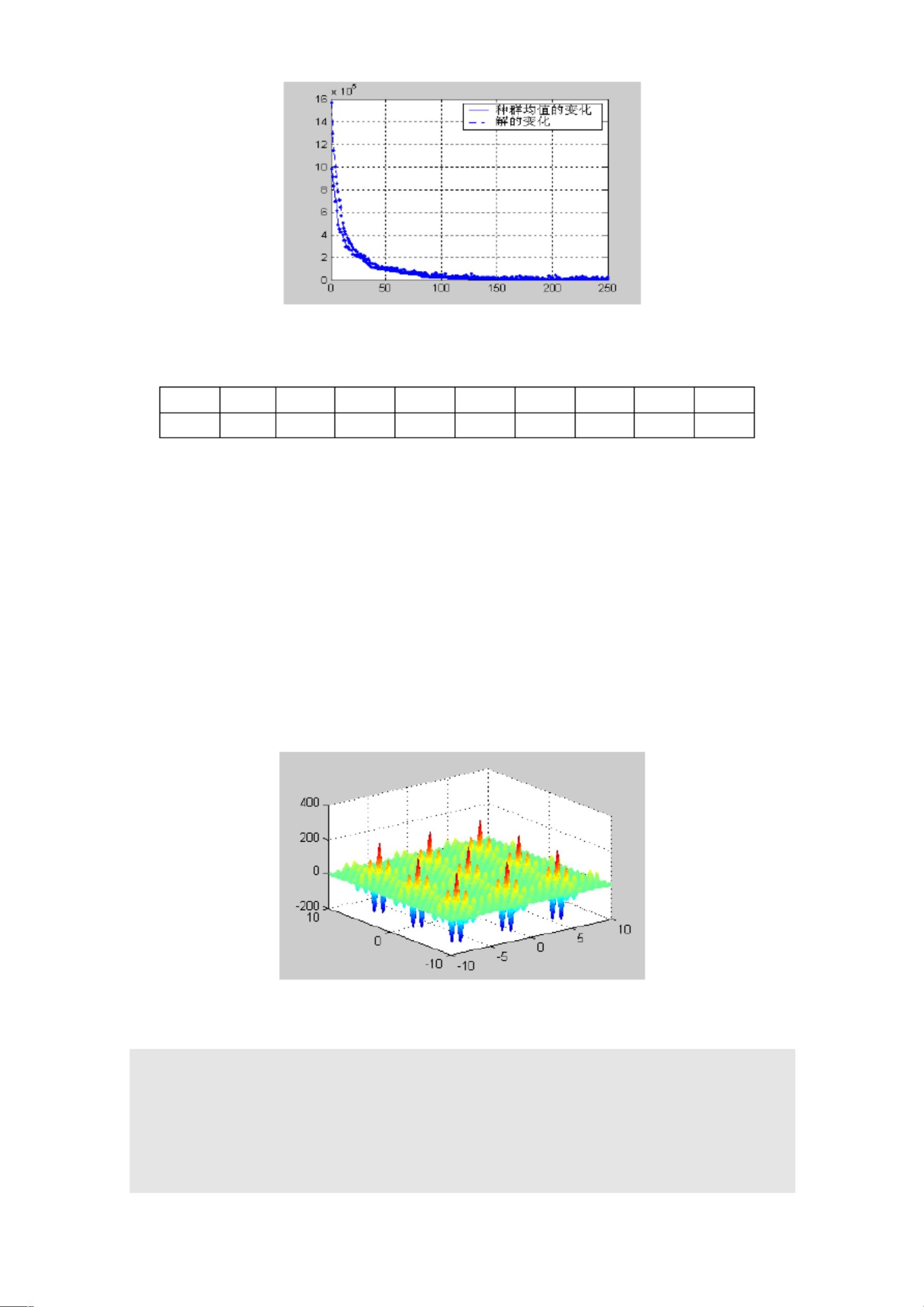
"第七章-遗传算法应用举例.doc.docx" 本文档主要介绍了如何利用遗传算法进行实际问题的求解，特别是在一元函数优化中的应用。遗传算法是一种模拟自然选择和遗传机制的全局优化方法，适合解决非线性、多模态、多目标等问题。其优势在于不需要对问题的具体特性有深入理解，只需定义合适的编码方式、选择、交叉和变异操作即可。 在描述的案例中，目标是找到函数 `f(x) = x*sin(10π*x) + 2.0` 在区间 [-1,2] 内的最大值。这个函数具有复杂的波动性质，传统优化方法可能难以找到全局最优解。遗传算法通过将实数编码为二进制，创建了一个种群，其中每个个体代表一个可能的解（即x值）。种群大小设置为40，每个个体的二进制位数（精度）为20，代沟（新一代与上一代的相似度）为0.9，最大遗传代数（迭代次数）为25。 在MATLAB程序中，首先画出函数曲线以便可视化。接着，定义了遗传算法的主要参数，包括个体数目、代沟、变量的二进制位数等。然后，通过选择、重组和变异操作来更新种群。选择操作使用的是“适者生存”策略（sus，即survival of the fittest），通过适应度值来决定哪些个体有机会进入下一代。重组和变异操作则引入新的变化，保持种群的多样性。 在每一代结束时，计算所有子代的目标函数值，并更新最佳解及其对应的种群序号。这一步骤包括将子代的二进制编码转换回十进制形式，以及计算目标函数值。遗传算法的性能通过跟踪最大适应度值和种群平均适应度值进行评估。 最后，程序输出最优解的x值及对应的目标函数值，并在函数图上标出最优解的位置。同时，绘制了适应度值随代数变化的曲线，展示算法的收敛过程。 这个例子展示了遗传算法在解决优化问题上的实用性，特别是在处理复杂函数时的优势。通过调整参数和编码方式，遗传算法可以应用于更广泛的领域，如多目标优化、组合优化、自动控制、机器人路径规划等。它提供了一种灵活且强大的工具，帮助我们寻找复杂问题的全局最优解决方案。