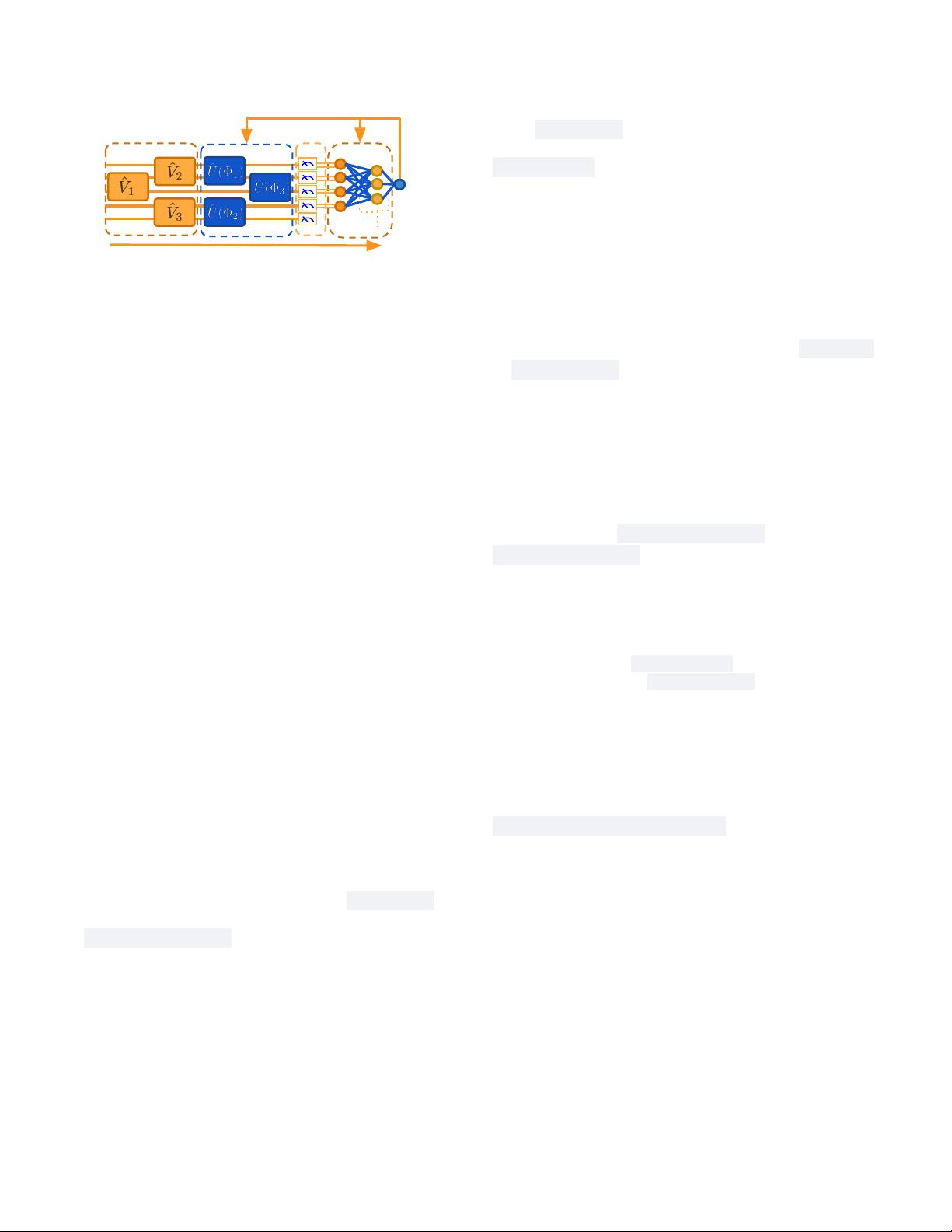
7
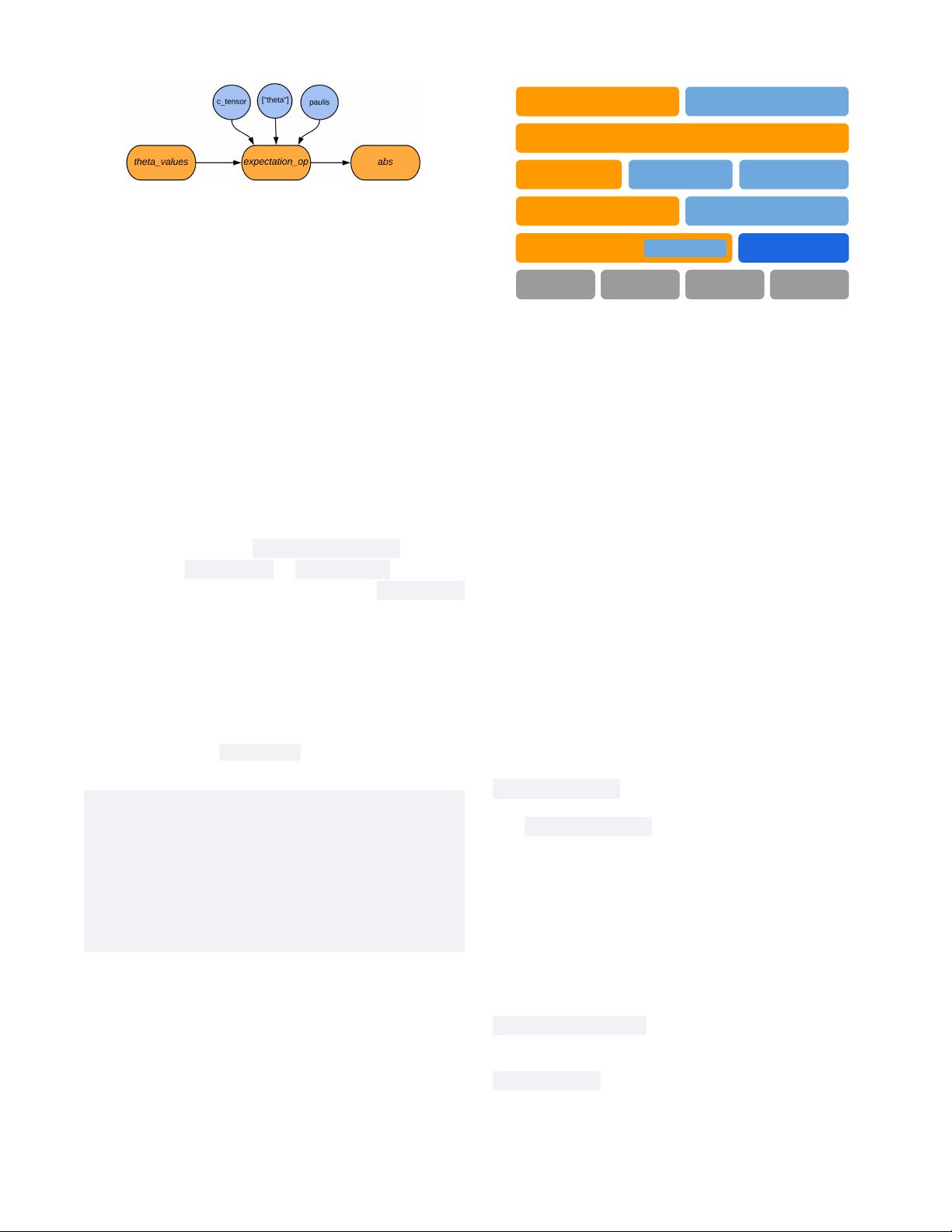
Figure 3. The TensorFlow graph generated to calculate the
expectation value of a parameterized circuit. The symbol
values can come from other TensorFlow ops, such as from
the outputs of a classical neural network. The output can be
passed on to other ops in the graph; here, for illustration, the
output is passed to the absolute value op.
to re-learn how to interface with quantum comput-
ers or re-learn how to solve problems using machine
learning.
First, we provide a bottom-up overview of TFQ to
provide intuition on how the framework functions at a
fundamental level. In TFQ, circuits and other quantum
computing constructs are tensors, and converting these
tensors into classical information via simulation or exe-
cution on a quantum device is done by ops. These ten-
sors are created by converting Cirq objects to TensorFlow
string tensors, using the tfq.convert_to_tensor function.
This takes in a cirq.Circuit or cirq.PauliSum object and
creates a string tensor representation. The cirq.Circuit
objects may be parameterized by SymPy symbols.
These tensors are then converted to classical informa-
tion via state simulation, expectation value calculation,
or sampling. TFQ provides ops for each of these compu-
tations. The following code snippet shows how a simple
parameterized circuit may be created using Cirq, and
its
ˆ
Z expectation evaluated at different parameter values
using the tfq expectation value calculation op. We feed
the output into the tf.math.abs op to show that tfq ops
integrate naively with tf ops.
qubit = cirq . Gri dQub it (0 , 0)
theta = sympy . Symb ol (’ theta ’)
c = cirq . C irc uit ( cirq .X( qub it ) ** the ta )
c_tens or = tfq . convert _ t o_tens o r ([ c] * 3)
the t a_va l ues = tf . c onst ant ([ [0] ,[1] ,[2]])
m = cirq .Z ( qubit )
pa uli s = tfq . conve r t _to_t e n sor ([ m] * 3)
exp e c tatio n _op = tfq . get_exp e c tation _ o p ()
ou tpu t = e xpect a t ion_o p (
c_tensor , [ ’ the ta ’] , t het a_v alu es , paulis )
abs _out p ut = tf . math . abs ( output )
We supply the expectation op with a tensor of parame-
terized circuits, a list of symbols contained in the circuits,
a tensor of values to use for those symbols, and tensor
operators to measure with respect to. Given this, it out-
puts a tensor of expectation values. The graph this code
generates is given by Fig. 3.
The expectation op is capable of running circuits on
a simulated backend, which can be a Cirq simulator or
our native TFQ simulator qsim (described in detail in
TF Keras Models
TF Layers
TF Execution Engine
TPU
Cirq
TFQ Ops
TFQ Layers
TFQ
Differentiators
TFQ
TensorFlow
Classical
hardware
Quantum
hardware
TFQ qsim
GPU
CPU
QPU
TF Ops
Classical Data:
integers/floats/strings
Quantum Data:
Circuits/Operators
Figure 4. The software stack of TFQ, showing its interactions
with TensorFlow, Cirq, and computational hardware. At the
top of the stack is the data to be processed. Classical data
is natively processed by TensorFlow; TFQ adds the ability to
process quantum data, consisting of both quantum circuits
and quantum operators. The next level down the stack is the
Keras API in TensorFlow. Since a core principle of TFQ is
native integration with core TensorFlow, in particular with
Keras models and optimizers, this level spans the full width
of the stack. Underneath the Keras model abstractions are
our quantum layers and differentiators, which enable hybrid
quantum-classical automatic differentiation when connected
with classical TensorFlow layers. Underneath the layers and
differentiators, we have TensorFlow ops, which instantiate the
dataflow graph. Our custom ops control quantum circuit ex-
ecution. The circuits can be run in simulation mode, by in-
voking qsim or Cirq, or eventually will be executed on QPU
hardware.
section II F), or on a real device. This is configured on
instantiation.
The expectation op is fully differentiable. Given
that there are many ways to calculate the gradient of
a quantum circuit with respect to its input parame-
ters, TFQ allows expectation ops to be configured with
one of many built-in differentiation methods using the
tfq.Differentiator interface, such as finite differencing,
parameter shift rules, and various stochastic methods.
The tfq.Differentiator interface also allows users to de-
fine their own gradient calculation methods for their spe-
cific problem if they desire.
The tensor representation of circuits and Paulis along
with the execution ops are all that are required to solve
any problem in QML. However, as a convenience, TFQ
provides an additional op for in-graph circuit construc-
tion. This was found to be convenient when solving prob-
lems where most of the circuit being run is static and
only a small part of it is being changed during train-
ing or inference. This functionality is provided by the
tfq.tfq_append_circuit op. It is expected that all but
the most dedicated users will never touch these low-
level ops, and instead will interface with TFQ using our
tf.keras.layers that provide a simplified interface.
The tools provided by TFQ can interact with both
core TensorFlow and, via Cirq, real quantum hardware.