支持向量机SVM入门解析
下载需积分: 16 | PDF格式 | 2.1MB |
更新于2024-07-22
| 141 浏览量 | 举报
"支持向量机通俗导论"
支持向量机(SVM,Support Vector Machine)是一种在机器学习领域广泛应用的监督学习算法,尤其在模式识别和分类问题上表现出色。该算法由Vapnik等人在90年代中期提出,基于统计学习理论,旨在通过最小化结构化风险来提升模型的泛化能力。
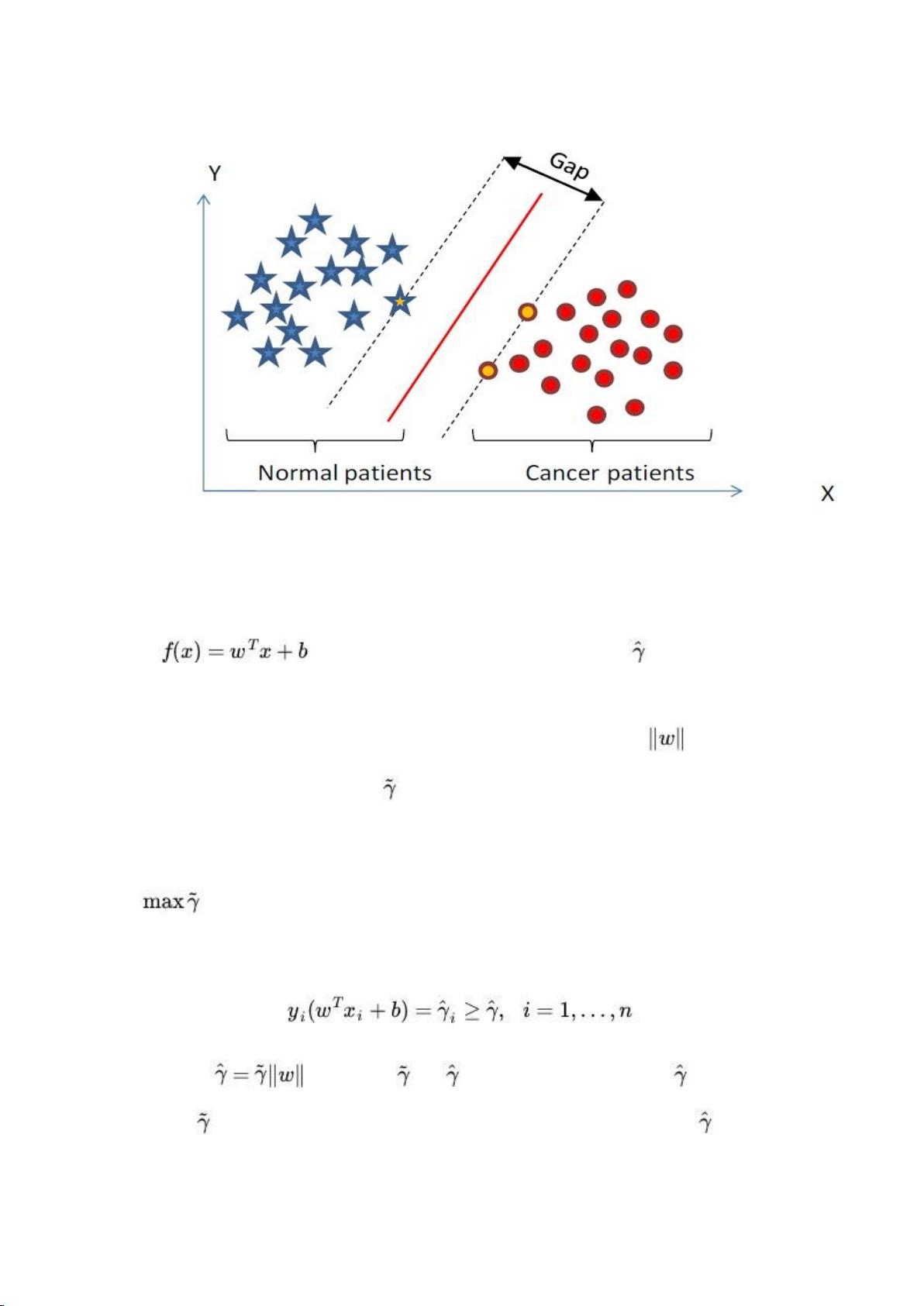
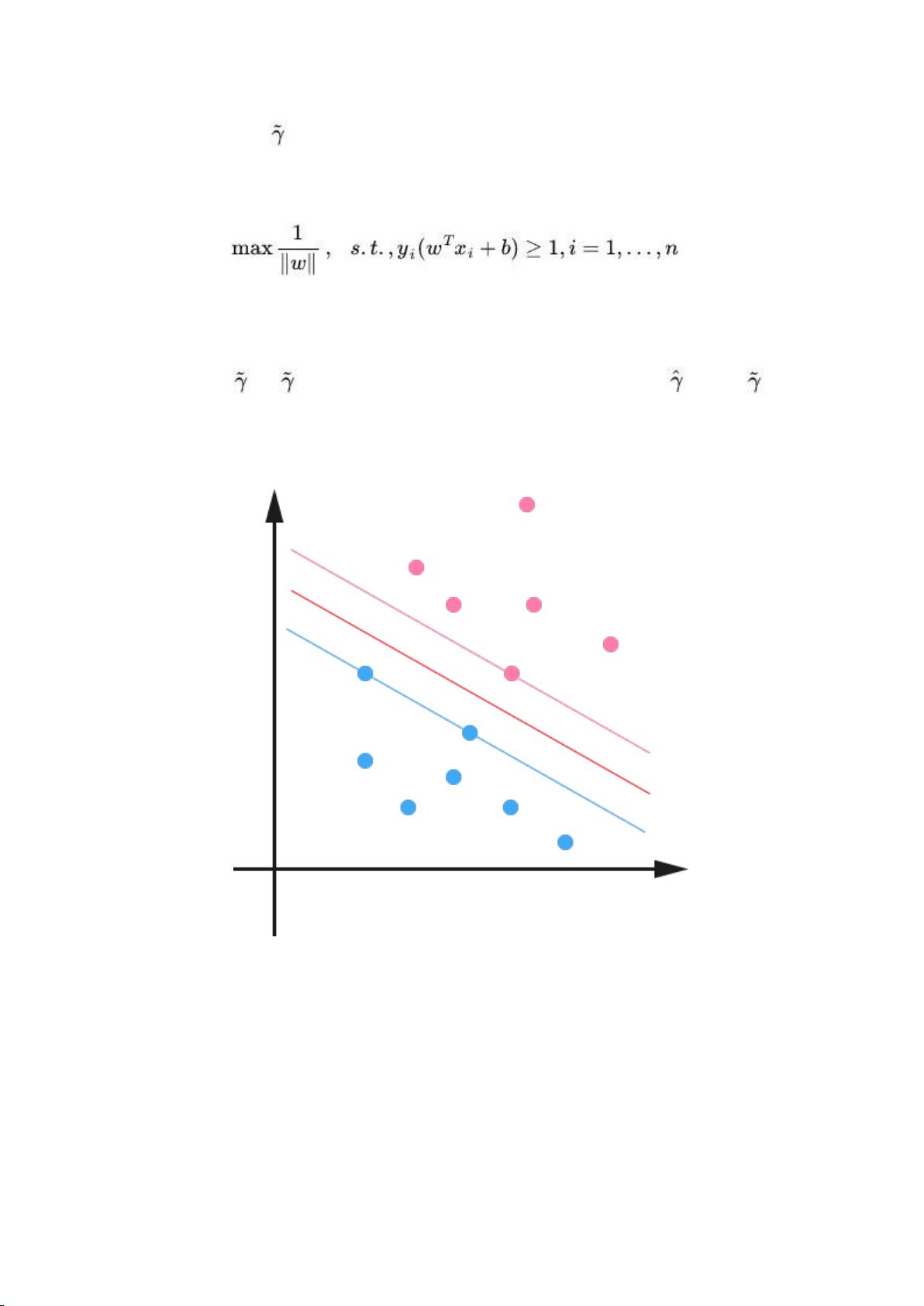
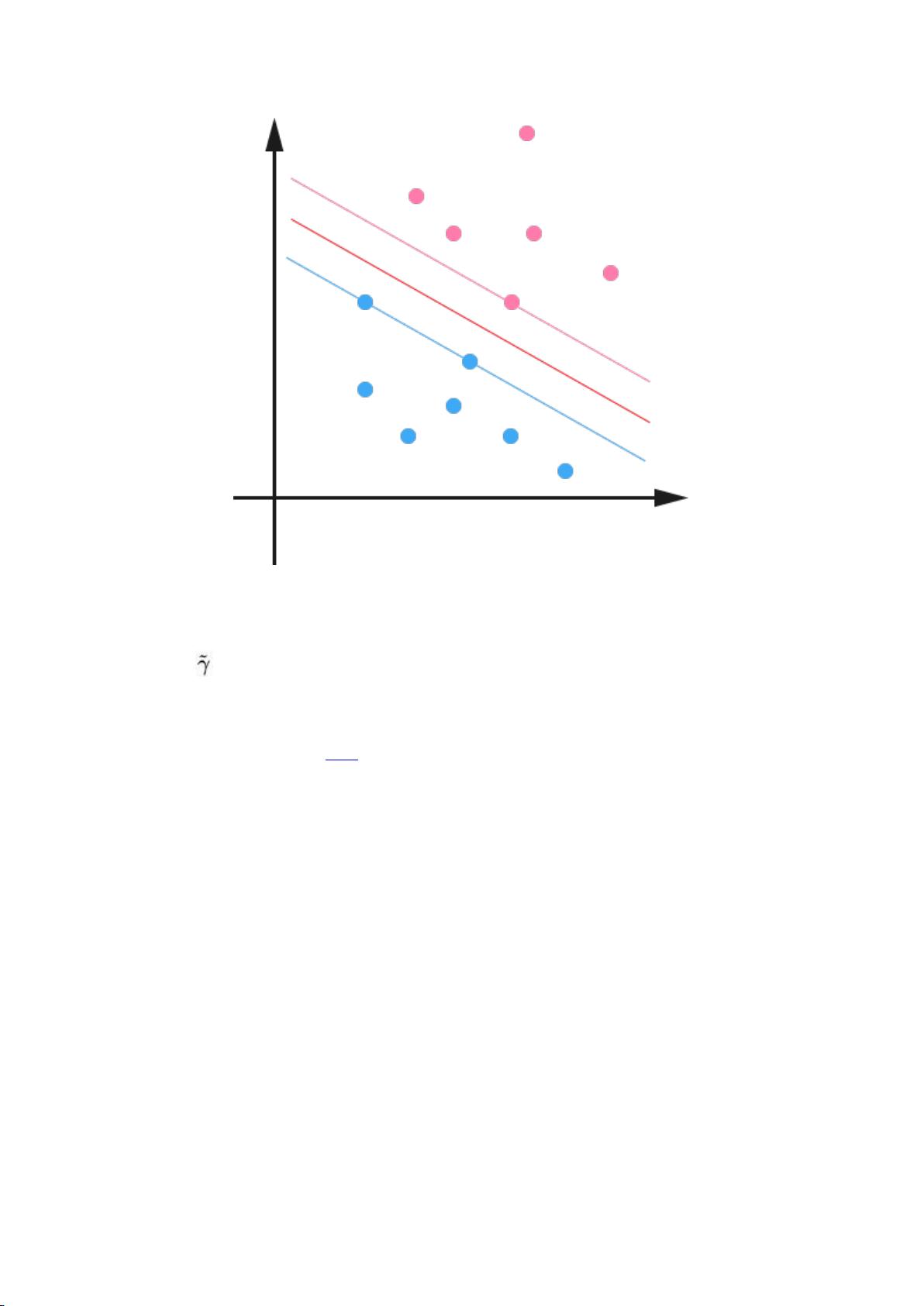
SVM的核心思想是找到一个最优的决策边界(超平面),能够将不同类别的样本点最大程度地分开。这个决策边界被称为最大间隔超平面。在二维空间中,我们可以直观地理解为找到一个直线,使得两类样本点分别位于直线的两侧,并且直线到最近的样本点(支持向量)的距离最大。在高维空间中,这个超平面可能是超曲面。
分类过程可以分为以下步骤:
1. **数据预处理**:对原始数据进行标准化或归一化,确保特征在同一尺度上,避免因特征尺度差异影响分类效果。
2. **构建超平面**:寻找最大化间隔的超平面。SVM使用核函数(如线性核、多项式核、高斯核/RBF等)将低维空间中的非线性可分问题转换为高维空间中的线性可分问题。
3. **支持向量**:距离超平面最近的样本点被称为支持向量,它们对确定超平面至关重要,因为超平面的位置由这些点决定。
4. **软间隔**:在实际问题中,数据可能并非完全线性可分。SVM引入了松弛变量和惩罚项,允许一些样本点落在决策边界内,但会受到一定的惩罚,即软间隔最大化。
5. **优化问题**:SVM通过解决一个凸二次规划问题来找到最优解,即最大间隔超平面。这涉及到求解拉格朗日乘子和对应的KKT条件。
6. **预测**:对于新的未知样本,根据其所属的超平面一侧来判断类别。
SVM的优势在于其泛化能力强,即使在小样本情况下也能得到较好的分类结果,同时能够处理高维数据。然而,它也有一些局限性,比如训练时间可能会随着样本数量增加而显著增长,特别是在大规模数据集上。此外,选择合适的核函数和参数调整也是SVM应用中的关键问题。
为了更好地理解SVM,读者可以借助数学工具,如 chrome 浏览器查看清晰的公式,动手推导关键定理和公式,例如拉格朗日乘子法、最大间隔公式等。同时,实践编程实现SVM算法,结合实际数据集进行训练和验证,将有助于深化理解和支持向量机在实际问题中的应用。
相关推荐









Michael__Shi
- 粉丝: 78

最新资源
- 基于优先级的进程调度模拟程序设计实现
- 专业转换工具:将Webex文件(WRF)高效转为WMV格式
- 在HTML5画布中利用Goraud着色渲染3D对象教程
- Android自定义顶部标题栏实现教程
- Facebook时光轴:发布、增加、删除功能解析
- 易语言VCL组合框功能扩展实现
- SPFDISK ver 3t:DOS分区工具与HDD BOOT区修改
- MATLAB实现人工神经网络识别英文字母
- VB纯物质化学性质数据库查询系统源码解析
- 探索vk.com的高效工具:vktools功能介绍与安装指南
- TPDesign4商业版智能家居控制面板免费下载
- 快速搭建与理解SpringBoot项目及其核心特性
- Java与C++混合编程实例演示
- Delphi/Kylix源码解析与实践应用
- 探索类似Windows开始菜单的压缩包功能
- 64位与32位lcc编译器实验使用指南