优化算法在八数码问题中的运用及分析
需积分: 11 38 浏览量
更新于2024-03-22
收藏 2.59MB PPTX 举报
八数码问题是一个经典的搜索问题,涉及到在一个3x3的棋盘上,将初始状态的数字按照规定的顺序移动到目标状态。为了解决这一问题,我们采用了多种算法进行求解,包括爬山法、随机重启爬山法、模拟退火法和遗传算法。
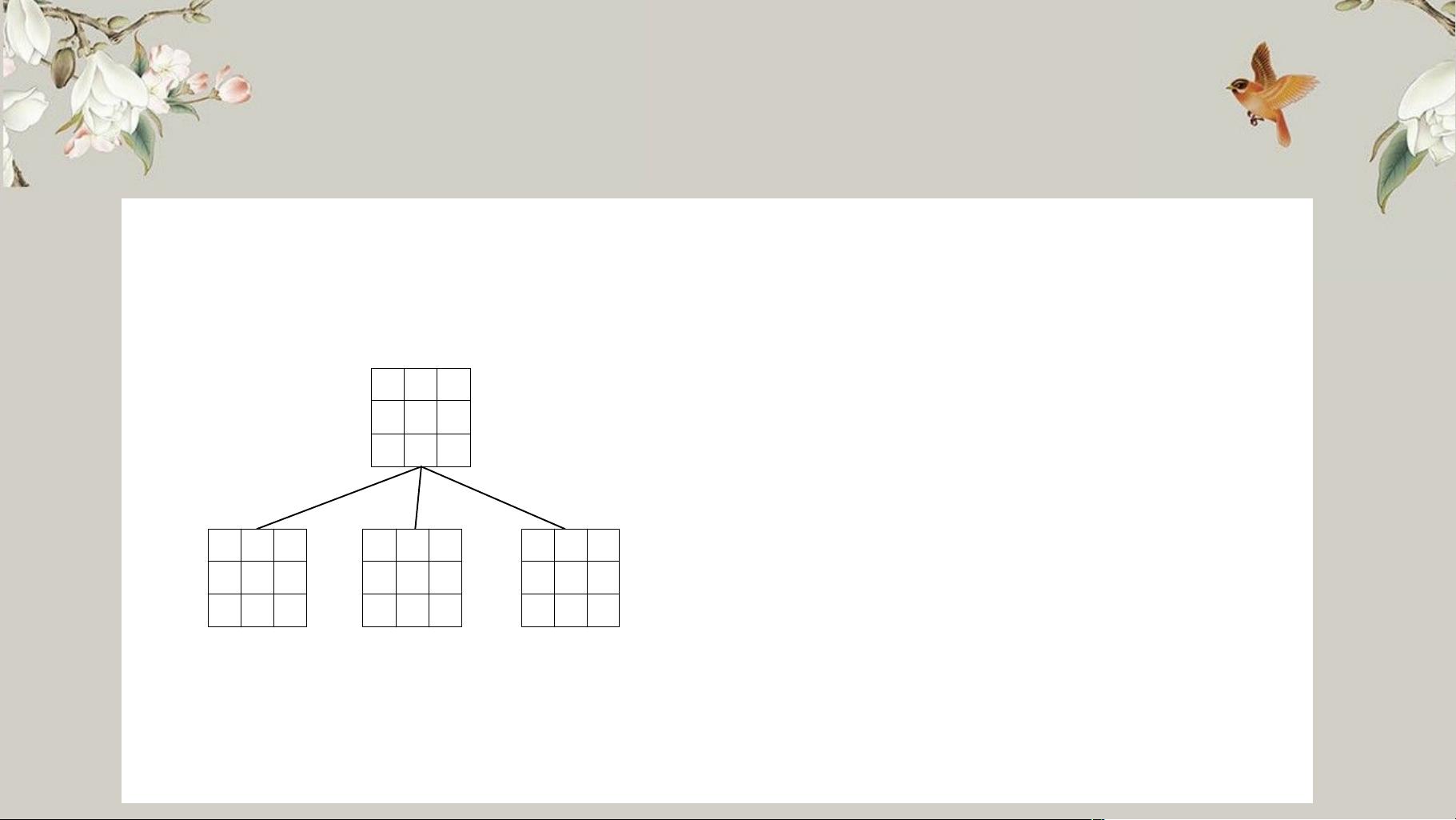
爬山法是一种简单的贪心搜索算法,每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。然而,这种方法容易陷入局部最优解,无法保证搜索到全局最优解。在解决八数码问题时,我们采用了评估函数来评估每个后继状态下的错误放置结点个数,选择其中错误放置结点个数最少的一个作为最优后继。通过不断评估和选择最优后继,直到错误放置的结点个数为0,即达到目标状态。
在具体求解八数码问题时,我们以初始状态2 0 3 1 6 4 8 7 5为例,目标状态为1 2 3 8 0 4 7 6 5。通过爬山法的迭代,我们逐步优化当前状态,将数字按照规定的顺序移动到目标状态。这一过程中,我们不断评估每个可能的后继状态,并选择最优状态,直至达到目标状态。
除了爬山法,我们还尝试了随机重启爬山法、模拟退火法和遗传算法来解决八数码问题。这些算法在搜索过程中采用不同的策略,如随机重启爬山法能够避免陷入局部最优解,模拟退火法则通过概率策略接受次优解以避免陷入局部最优解,而遗传算法则模拟遗传过程进行搜索。
通过对比这些算法的表现,我们可以发现不同算法在解决八数码问题时的效率和质量有所差异。其中,遗传算法可能会在搜索过程中产生更优的解,而爬山法和模拟退火法可能更适合于简单问题的求解。因此,在实际应用中,我们可以根据具体问题的性质和需求选择合适的算法来解决。
总的来说,八数码问题是一个经典的搜索问题,可以通过多种算法进行求解。不同算法在搜索过程中有各自的优劣势,我们需要根据具体情况选取合适的算法来解决问题,以获得更好的效果。通过对比和总结不同算法的表现,我们可以更好地理解和运用这些算法,拓展我们的解决问题的方法和思路。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2021-10-14 上传
2021-10-12 上传
2021-09-23 上传
2021-09-23 上传
2021-09-24 上传
2021-09-23 上传
dear_queen
- 粉丝: 143
最新资源
- 前端技术分享:全面的JavaScript 示例教程
- Ruby项目active_admin_sample部署与运行指南
- 重播扑克Replay Bankroll Chart-crx插件使用指南
- Android基础实例解析:天气、地图、音乐播放器等源码
- JCms v1.5.3:Asp.NET内容管理系统助力电子政务与校园门户建设
- Apache Beam MySQL连接器:轻松读取MySQL数据库数据
- 深入解析词云技术在网络文本分析中的应用
- Node.js环境下hyperdb分布式数据库的应用与扩展
- 网络性能测试与评估:tp-at-arq_redes_infnet深入分析
- 掌握Python数据结构:问题集练习指南
- 基于BART模型的神经故事生成技术研究
- 前端美化神器:Ion.RangeSlider实现及示例解析
- C++实现3DES与Base64加解密方法示例
- 探索Dodger.js:Vimscript下的JavaScript开发利器
- Python打包服务器项目实现自动化发布与一键部署
- Python实践教程:HuohuaTest01压缩包子文件解析