Mathematica作图指南：函数、数据与参数图形

"Mathematica是一款强大的数学软件，用于函数图形描绘和数据分析。本文主要介绍了Mathematica在二维函数作图、数据集合的图形以及二维参数作图方面的应用。 在二维函数作图方面，Mathematica提供了Plot命令来绘制一元或多元函数的图形。基本语法为`Plot[f, {x, xmin, xmax}, option->value]`，其中`f`是函数表达式，`xmin`和`xmax`定义了x轴的范围。用户可以通过设置不同的选项来定制图形的细节，如图形比例、坐标轴标签、图形标题、绘图范围、样式和点数等。例如，`AspectRatio`用于调整图形的高宽比，`AxesLabel`和`PlotLabel`分别用于添加坐标轴名称和图形标题，`PlotRange`用于指定因变量的显示范围，`PlotStyle`用于定义线条颜色和粗细，而`PlotPoints`则控制绘图时计算的点数。 具体示例中，我们看到如何绘制函数图形，如何取消坐标轴刻度，添加自定义坐标轴名称，标注图形交点和名称，以及自定义特定轴的刻度范围。此外，通过`Show`命令可以延迟显示图形。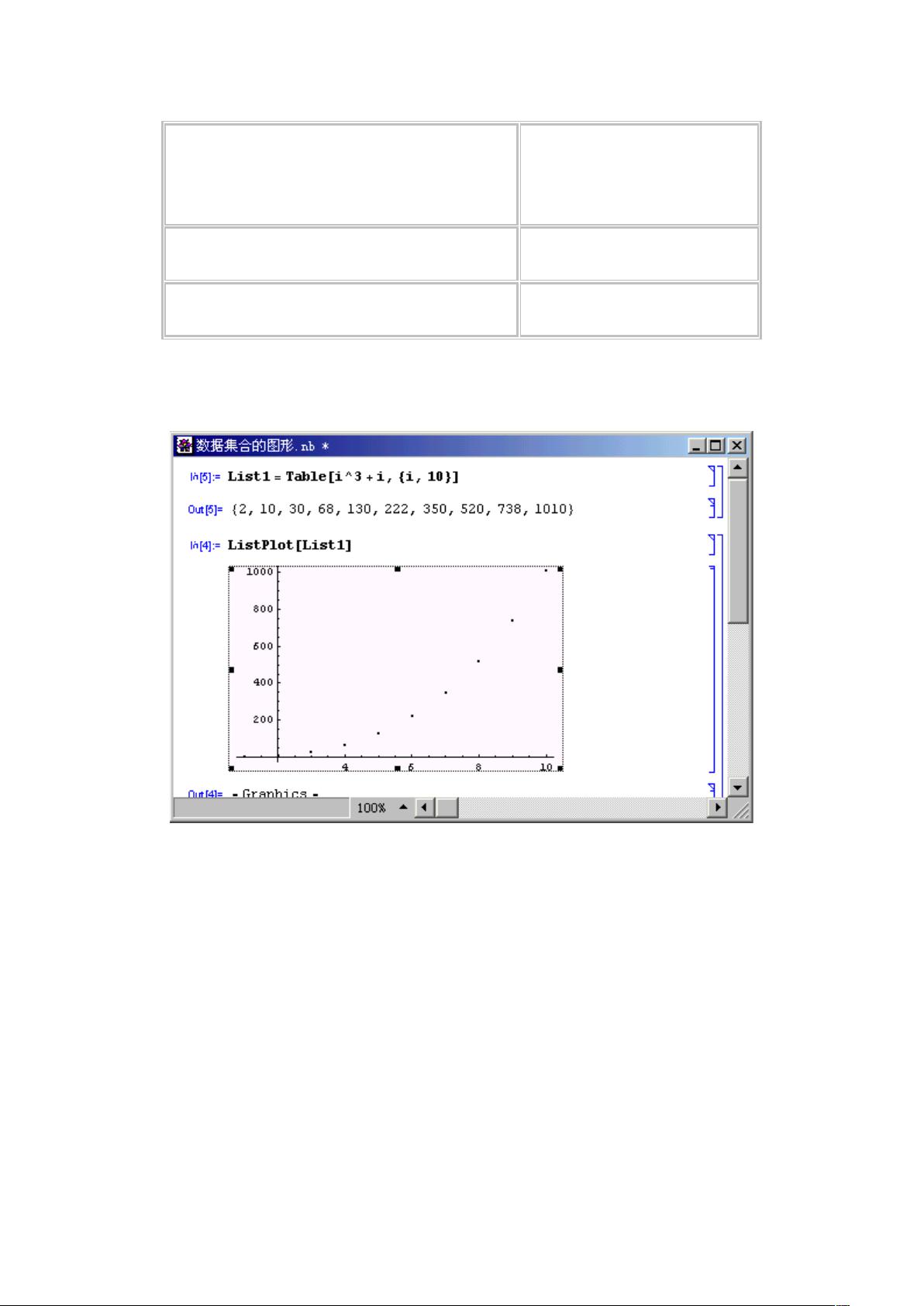 对于数据集合的图形，Mathematica提供了`ListPlot`命令。当数据是以序列形式给出时，`ListPlot[{y1, y2, ...}]`会绘制每个x值对应的y值图形；而`ListPlot[{{x1, y1}, {x2, y2}, ...}]`则用于绘制离散点；若希望将离散点连成曲线，可以设置`PlotJoined->True`。例如，一个离散数据集的图形可以通过`ListPlot`命令轻松呈现。 二维参数作图是Mathematica的另一强大功能，它允许我们根据参数绘制函数图形。这在处理与时间或其他参数相关的函数时特别有用。尽管这里没有提供具体的参数作图例子，但可以想象，通过将参数引入到`Plot`命令中，可以创建动态变化的图形，展示参数变化对函数图形的影响。 Mathematica是一个功能丰富的工具，不仅能够进行复杂的数学运算，还能以直观的方式展示这些计算结果。无论是函数的连续图形还是离散数据的可视化，或是参数依赖的图形，Mathematica都能提供灵活的控制和高质量的输出，是科学研究和教学中不可或缺的工具。"